在MoonBit中实现IntMap

2025年12月10日 · 阅读需 8 分钟

键值对容器是现代编程语言必备的标准库成员之一，它应用广泛，所以其基本操作的性能非常重要。函数式语言的键值对容器实现大多基于某种平衡二叉搜索树，这样实现的键值对容器在查找和插入操作上表现优秀，但在需要合并两个键值对容器时表现不佳，命令式语言常用的哈希表也不擅长合并操作。

IntMap是一种为整数特化的不可变键值对容器，它只能以整数为键，通过牺牲一定的通用性，它实现了高效的合并/取交集操作。本文将从最朴素的二叉字典树开始，逐步改进到IntMap.

二叉字典树

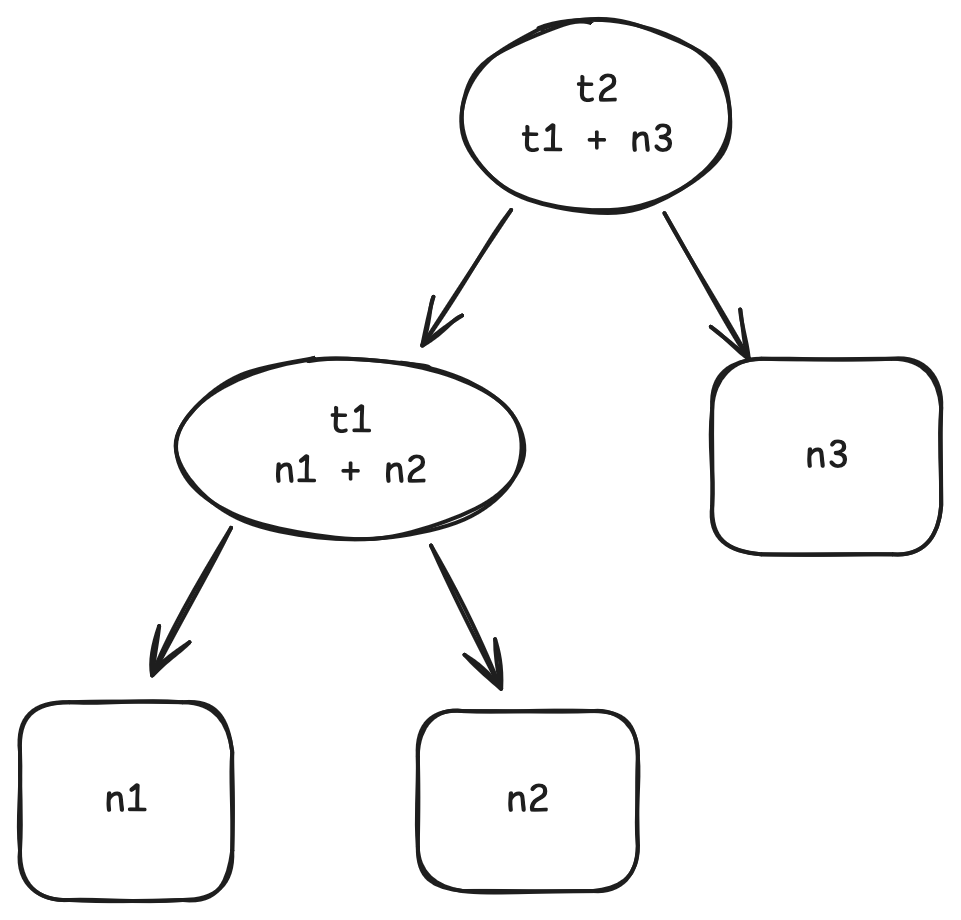
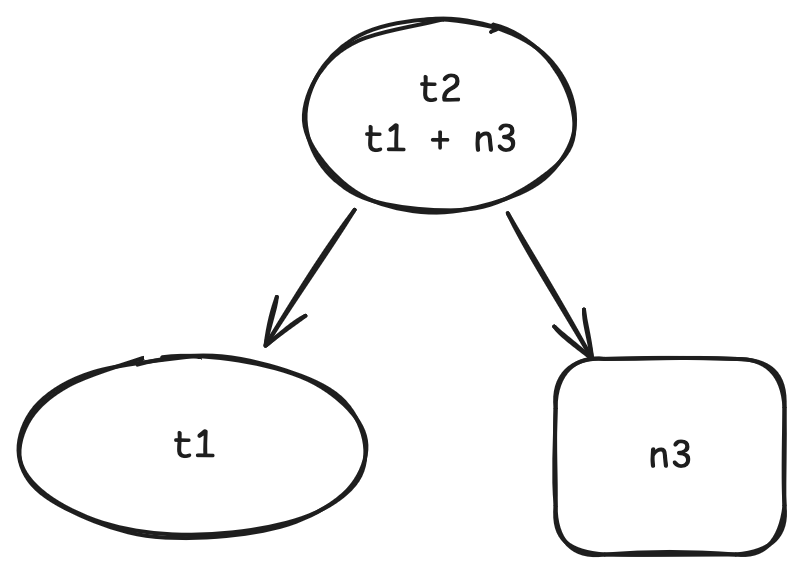
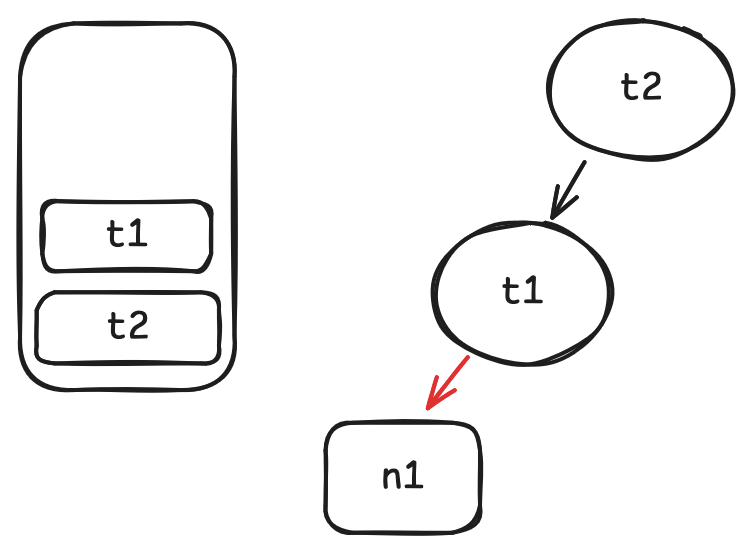
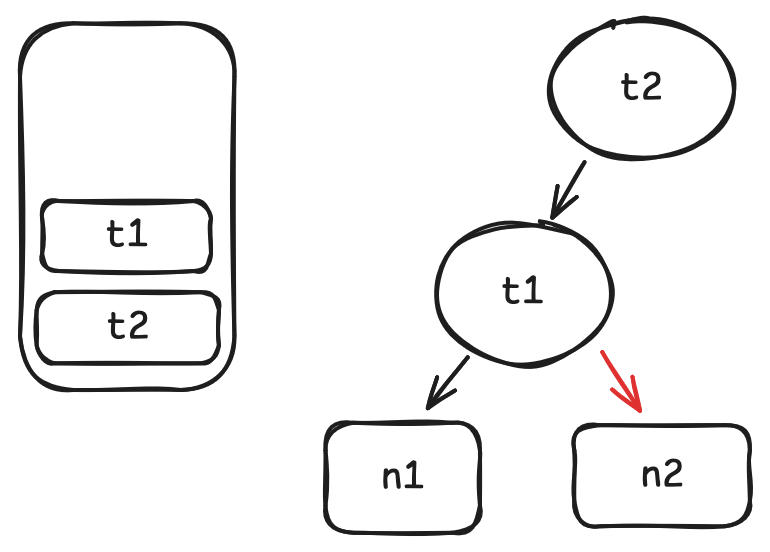
二叉字典树是一种使用每个键的二进制表示决定其位置的二叉树，键的二进制表示是一长串有限的0和1，那么假如当前位是0，就向左子树递归，当前位为1则向右子树递归.

///|
enum BinTrie[T] {
  BinTrie[T]
Empty
  (T) -> BinTrie[T]
Leaf(type parameter T
T)
  (left~ : BinTrie[T], right~ : BinTrie[T]) -> BinTrie[T]
Branch(BinTrie[T]
left~ : enum BinTrie[T] {
  Empty
  Leaf(T)
  Branch(left~ : BinTrie[T], right~ : BinTrie[T])
}
BinTrie[type parameter T
T], BinTrie[T]
right~ : enum BinTrie[T] {
  Empty
  Leaf(T)
  Branch(left~ : BinTrie[T], right~ : BinTrie[T])
}
BinTrie[type parameter T
T])
}

要在二叉字典树里查找某个键对应的值，只需要依次读取键的二进制位，根据其值选择向左或者向右移动，直到到达某个叶子节点

此处读取二进制位的顺序是从整数最小位到最高位

fn[T] enum BinTrie[T] {
  Empty
  Leaf(T)
  Branch(left~ : BinTrie[T], right~ : BinTrie[T])
}
BinTrie::fn[T] BinTrie::lookup(self : BinTrie[T], key : UInt) -> T?
lookup(BinTrie[T]
self : enum BinTrie[T] {
  Empty
  Leaf(T)
  Branch(left~ : BinTrie[T], right~ : BinTrie[T])
}
BinTrie[type parameter T
T], UInt
key : UInt
UInt) -> type parameter T
T? {
  match BinTrie[T]
self {
    BinTrie[T]
Empty => T?
None
    (T) -> BinTrie[T]
Leaf(T
value) => (T) -> T?
Some(T
value)
    (left~ : BinTrie[T], right~ : BinTrie[T]) -> BinTrie[T]
Branch(BinTrie[T]
left~, BinTrie[T]
right~) =>
      if UInt
key fn Mod::mod(self : UInt, other : UInt) -> UInt
Calculates the remainder of dividing one unsigned integer by another.
Parameters:

self : The unsigned integer dividend.
other : The unsigned integer divisor.
Returns the remainder of the division operation.
Throws a panic if other is zero.
Example:
let a = 17U
let b = 5U
inspect(a % b, content="2") // 17 divided by 5 gives quotient 3 and remainder 2
inspect(7U % 4U, content="3")
% 2U fn Eq::equal(self : UInt, other : UInt) -> Bool
Compares two unsigned 32-bit integers for equality.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand to compare with.
Returns true if both integers have the same value, false otherwise.
Example:
let a = 42U
let b = 42U
let c = 24U
inspect(a == b, content="true")
inspect(a == c, content="false")
== 0 {
        BinTrie[T]
left.fn[T] BinTrie::lookup(self : BinTrie[T], key : UInt) -> T?
lookup(UInt
key fn Div::div(self : UInt, other : UInt) -> UInt
Performs division between two unsigned 32-bit integers. The operation follows
standard unsigned integer division rules, where the result is truncated
towards zero.
Parameters:

self : The dividend (the number to be divided).
other : The divisor (the number to divide by).
Returns an unsigned 32-bit integer representing the quotient of the division.
Example:
let a = 42U
let b = 5U
inspect(a / b, content="8") // Using infix operator
/ 2)
      } else {
        BinTrie[T]
right.fn[T] BinTrie::lookup(self : BinTrie[T], key : UInt) -> T?
lookup(UInt
key fn Div::div(self : UInt, other : UInt) -> UInt
Performs division between two unsigned 32-bit integers. The operation follows
standard unsigned integer division rules, where the result is truncated
towards zero.
Parameters:

self : The dividend (the number to be divided).
other : The divisor (the number to divide by).
Returns an unsigned 32-bit integer representing the quotient of the division.
Example:
let a = 42U
let b = 5U
inspect(a / b, content="8") // Using infix operator
/ 2)
      }
  }
}

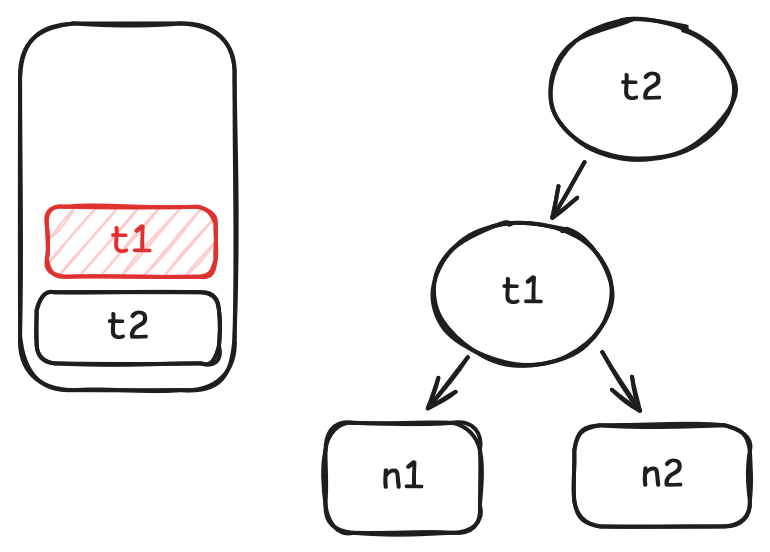
为了避免创建过多空树，我们不直接调用值构造子，而是使用branch方法

fn[T] enum BinTrie[T] {
  Empty
  Leaf(T)
  Branch(left~ : BinTrie[T], right~ : BinTrie[T])
}
BinTrie::fn[T] BinTrie::br(left : BinTrie[T], right : BinTrie[T]) -> BinTrie[T]
br(BinTrie[T]
left : enum BinTrie[T] {
  Empty
  Leaf(T)
  Branch(left~ : BinTrie[T], right~ : BinTrie[T])
}
BinTrie[type parameter T
T], BinTrie[T]
right : enum BinTrie[T] {
  Empty
  Leaf(T)
  Branch(left~ : BinTrie[T], right~ : BinTrie[T])
}
BinTrie[type parameter T
T]) -> enum BinTrie[T] {
  Empty
  Leaf(T)
  Branch(left~ : BinTrie[T], right~ : BinTrie[T])
}
BinTrie[type parameter T
T] {
  match (BinTrie[T]
left, BinTrie[T]
right) {
    (BinTrie[T]
Empty, BinTrie[T]
Empty) => BinTrie[T]
Empty
    _ => (left~ : BinTrie[T], right~ : BinTrie[T]) -> BinTrie[T]
Branch(BinTrie[T]
left~, BinTrie[T]
right~)
  }
}

Patricia Tree

Patricia Tree在二叉字典树的基础上保存了更多信息以加速查找,在每个分叉的地方，它都保留子树中所有键的公共前缀(虽然此处是从最低位开始计算，但我们仍然使用前缀这种说法)，并用一个无符号整数标记当前的分支位(branching bit).这样一来，查找时需要经过的分支数量大大减少。

///|
enum PatriciaTree[T] {
  PatriciaTree[T]
Empty
  (key~ : Int, value~ : T) -> PatriciaTree[T]
Leaf(Int
key~ : Int
Int, T
value~ : type parameter T
T)
  (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(
    UInt
prefix~ : UInt
UInt,
    UInt
mask~ : UInt
UInt,
    PatriciaTree[T]
left~ : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T],
    PatriciaTree[T]
right~ : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T]
  )
}

///|
fn[T] enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree::fn[T] PatriciaTree::lookup(self : PatriciaTree[T], key : Int) -> T?
lookup(PatriciaTree[T]
self : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T], Int
key : Int
Int) -> type parameter T
T? {
  match PatriciaTree[T]
self {
    PatriciaTree[T]
Empty => T?
None
    (key~ : Int, value~ : T) -> PatriciaTree[T]
Leaf(Int
key=Int
k, T
value~) => if Int
k fn Eq::equal(self : Int, other : Int) -> Bool
Compares two integers for equality.
Parameters:

self : The first integer to compare.
other : The second integer to compare.
Returns true if both integers have the same value, false otherwise.
Example:
inspect(42 == 42, content="true")
inspect(42 == -42, content="false")
== Int
key { (T) -> T?
Some(T
value) } else { T?
None }
    (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix~, UInt
mask~, PatriciaTree[T]
left~, PatriciaTree[T]
right~) =>
      if Bool
!fn match_prefix(key~ : UInt, prefix~ : UInt, mask~ : UInt) -> Bool
match_prefixBool
(UInt
keyBool
=Int
keyBool
.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uintBool
(), UInt
prefixBool
~, UInt
maskBool
~) {
        T?
None
      } else if fn zero(k : UInt, mask~ : UInt) -> Bool
zero(Int
key.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint(), UInt
mask~) {
        PatriciaTree[T]
left.fn[T] PatriciaTree::lookup(self : PatriciaTree[T], key : Int) -> T?
lookup(Int
key)
      } else {
        PatriciaTree[T]
right.fn[T] PatriciaTree::lookup(self : PatriciaTree[T], key : Int) -> T?
lookup(Int
key)
      }
  }
}

///|
fn fn get_prefix(key : UInt, mask~ : UInt) -> UInt
get_prefix(UInt
key : UInt
UInt, UInt
mask~ : UInt
UInt) -> UInt
UInt {
  UInt
key fn BitAnd::land(self : UInt, other : UInt) -> UInt
Performs a bitwise AND operation between two unsigned 32-bit integers. For
each bit position, the result is 1 if the bits at that position in both
operands are 1, and 0 otherwise.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns an unsigned 32-bit integer representing the result of the bitwise AND
operation.
Example:
let a = 0xF0F0U // 1111_0000_1111_0000
let b = 0xFF00U // 1111_1111_0000_0000
inspect(a & b, content="61440") // 1111_0000_0000_0000 = 61440
& (UInt
mask fn Sub::sub(self : UInt, other : UInt) -> UInt
Performs subtraction between two unsigned 32-bit integers. When the result
would be negative, the function wraps around using modular arithmetic (2^32).
Parameters:

self : The first unsigned 32-bit integer (minuend).
other : The second unsigned 32-bit integer to subtract from the first
(subtrahend).
Returns a new unsigned 32-bit integer representing the difference between the
two numbers. If the result would be negative, it wraps around to a positive
number by adding 2^32 repeatedly until the result is in range.
Example:
let a = 5U
let b = 3U
inspect(a - b, content="2")
let c = 3U
let d = 5U
inspect(c - d, content="4294967294") // wraps around to 2^32 - 2
- 1U)
}

///|
fn fn match_prefix(key~ : UInt, prefix~ : UInt, mask~ : UInt) -> Bool
match_prefix(UInt
key~ : UInt
UInt, UInt
prefix~ : UInt
UInt, UInt
mask~ : UInt
UInt) -> Bool
Bool {
  fn get_prefix(key : UInt, mask~ : UInt) -> UInt
get_prefix(UInt
key, UInt
mask~) fn Eq::equal(self : UInt, other : UInt) -> Bool
Compares two unsigned 32-bit integers for equality.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand to compare with.
Returns true if both integers have the same value, false otherwise.
Example:
let a = 42U
let b = 42U
let c = 24U
inspect(a == b, content="true")
inspect(a == c, content="false")
== UInt
prefix
}

///|
fn fn zero(k : UInt, mask~ : UInt) -> Bool
zero(UInt
k : UInt
UInt, UInt
mask~ : UInt
UInt) -> Bool
Bool {
  (UInt
k fn BitAnd::land(self : UInt, other : UInt) -> UInt
Performs a bitwise AND operation between two unsigned 32-bit integers. For
each bit position, the result is 1 if the bits at that position in both
operands are 1, and 0 otherwise.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns an unsigned 32-bit integer representing the result of the bitwise AND
operation.
Example:
let a = 0xF0F0U // 1111_0000_1111_0000
let b = 0xFF00U // 1111_1111_0000_0000
inspect(a & b, content="61440") // 1111_0000_0000_0000 = 61440
& UInt
mask) fn Eq::equal(self : UInt, other : UInt) -> Bool
Compares two unsigned 32-bit integers for equality.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand to compare with.
Returns true if both integers have the same value, false otherwise.
Example:
let a = 42U
let b = 42U
let c = 24U
inspect(a == b, content="true")
inspect(a == c, content="false")
== 0
}

现在branch方法可以做更多优化, 保证Branch节点的子树不含Empty.

///|
fn[T] enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree::fn[T] PatriciaTree::branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
branch(
  UInt
prefix~ : UInt
UInt,
  UInt
mask~ : UInt
UInt,
  PatriciaTree[T]
left~ : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T],
  PatriciaTree[T]
right~ : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T],
) -> enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T] {
  match (PatriciaTree[T]
left, PatriciaTree[T]
right) {
    (PatriciaTree[T]
Empty, PatriciaTree[T]
right) => PatriciaTree[T]
right
    (PatriciaTree[T]
left, PatriciaTree[T]
Empty) => PatriciaTree[T]
left
    _ => (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix~, UInt
mask~, PatriciaTree[T]
left~, PatriciaTree[T]
right~)
  }
}

插入与合并

既然类型定义已经确定，接下来要做的就是实现插入和合并操作。由于插入操作也可以看作将一个只有一个叶节点的树与原本的树合并，所以我们优先介绍合并操作的实现。

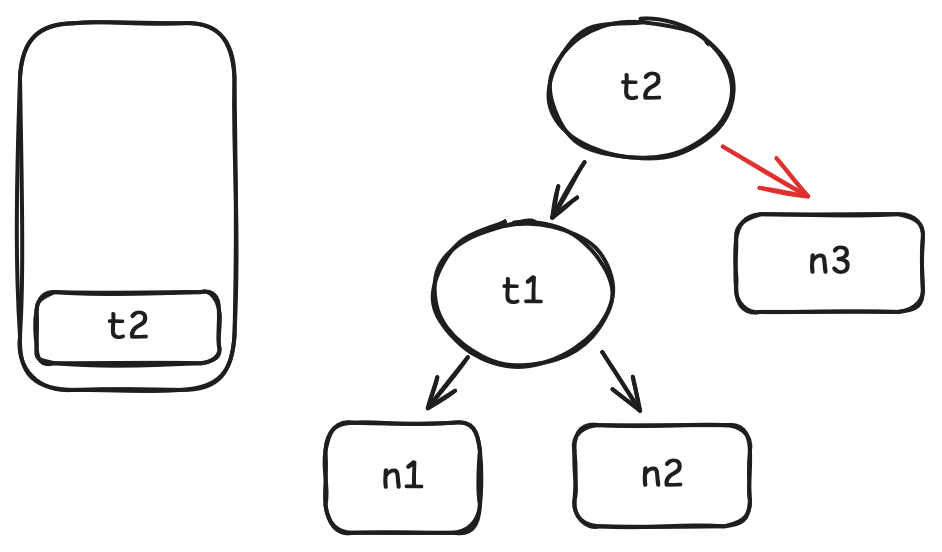
我们首先讨论可以走捷径的情况：假设我们有两个非空树t0和t1，它们的最长公共前缀分别为p0和p1且p0和p1互不包含, 那么不管t0和t1有多大，合并它们的成本都是一样的，因为只需要创建一个新的Branch节点。我们通过辅助函数join来实现。

生成掩码的函数gen_mask利用了整数二进制补码的一个特性来寻找最低的分支位。

假设输入x的二进制表示为

00100100000

那么，x.lnot()得到

11011011111

加一得到

11011100000

跟原来的x进行按位与后，得到：

00000100000

///|
fn[T] fn[T] join(p0 : UInt, t0 : PatriciaTree[T], p1 : UInt, t1 : PatriciaTree[T]) -> PatriciaTree[T]
join(
  UInt
p0 : UInt
UInt,
  PatriciaTree[T]
t0 : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T],
  UInt
p1 : UInt
UInt,
  PatriciaTree[T]
t1 : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T],
) -> enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T] {
  let UInt
mask = fn gen_mask(p0 : UInt, p1 : UInt) -> UInt
gen_mask(UInt
p0, UInt
p1)
  if fn zero(k : UInt, mask~ : UInt) -> Bool
zero(UInt
p0, UInt
mask~) {
    PatriciaTree::(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix=fn get_prefix(key : UInt, mask~ : UInt) -> UInt
get_prefix(UInt
p0, UInt
mask~), UInt
mask~, PatriciaTree[T]
left=PatriciaTree[T]
t0, PatriciaTree[T]
right=PatriciaTree[T]
t1)
  } else {
    PatriciaTree::(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix=fn get_prefix(key : UInt, mask~ : UInt) -> UInt
get_prefix(UInt
p0, UInt
mask~), UInt
mask~, PatriciaTree[T]
left=PatriciaTree[T]
t1, PatriciaTree[T]
right=PatriciaTree[T]
t0)
  }
}

///|
fn fn gen_mask(p0 : UInt, p1 : UInt) -> UInt
gen_mask(UInt
p0 : UInt
UInt, UInt
p1 : UInt
UInt) -> UInt
UInt {
  fn (UInt) -> UInt
lowest_bit(UInt
x : UInt
UInt) -> UInt
UInt {
    UInt
x fn BitAnd::land(self : UInt, other : UInt) -> UInt
Performs a bitwise AND operation between two unsigned 32-bit integers. For
each bit position, the result is 1 if the bits at that position in both
operands are 1, and 0 otherwise.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns an unsigned 32-bit integer representing the result of the bitwise AND
operation.
Example:
let a = 0xF0F0U // 1111_0000_1111_0000
let b = 0xFF00U // 1111_1111_0000_0000
inspect(a & b, content="61440") // 1111_0000_0000_0000 = 61440
& (UInt
x.fn UInt::reinterpret_as_int(self : UInt) -> Int
reinterpret the unsigned int as signed int
For number within the range of 0..=2^31-1,
the value is the same. For number within the range of 2^31..=2^32-1,
the value is negative
reinterpret_as_int().fn Neg::neg(self : Int) -> Int
Performs arithmetic negation on an integer value, returning its additive
inverse.
Parameters:

self : The integer value to negate.
Returns the negation of the input value. For all inputs except
Int::min_value(), returns the value with opposite sign. When the input is
Int::min_value(), returns Int::min_value() due to two's complement
representation.
Example:
inspect(-42, content="-42")
inspect(42, content="42")
inspect(2147483647, content="2147483647") // negating near min value
neg().fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint())
  }

  (UInt) -> UInt
lowest_bit(UInt
p0 fn BitXOr::lxor(self : UInt, other : UInt) -> UInt
Performs a bitwise XOR (exclusive OR) operation between two unsigned 32-bit
integers. Each bit in the result is set to 1 if the corresponding bits in the
operands are different, and 0 if they are the same.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns the result of the bitwise XOR operation.
Example:
let a = 0xFF00U // Binary: 1111_1111_0000_0000
let b = 0x0F0FU // Binary: 0000_1111_0000_1111
inspect(a ^ b, content="61455") // Binary: 1111_0000_0000_1111
^ UInt
p1)
}

万事俱备，现在可以开始编写insert_with函数了。对Empty和Leaf分支的处理都非常直接，而对于Branch, 在前缀互不包含时调用join，其他情况则根据分支位选择一个分支递归下去。

///|
fn[T] enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree::fn[T] PatriciaTree::insert_with(self : PatriciaTree[T], k : Int, v : T, combine~ : (T, T) -> T) -> PatriciaTree[T]
insert_with(
  PatriciaTree[T]
self : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T],
  Int
k : Int
Int,
  T
v : type parameter T
T,
  (T, T) -> T
combine~ : (type parameter T
T, type parameter T
T) -> type parameter T
T,
) -> enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T] {
  fn (PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
tree : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T]) -> enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T] {
    match PatriciaTree[T]
tree {
      PatriciaTree[T]
Empty => (key~ : Int, value~ : T) -> PatriciaTree[T]
Leaf(Int
key=Int
k, T
value=T
v)
      (key~ : Int, value~ : T) -> PatriciaTree[T]
LeafPatriciaTree[T]
(Int
keyPatriciaTree[T]
~, T
valuePatriciaTree[T]
~) as tree =>
        if Int
key fn Eq::equal(self : Int, other : Int) -> Bool
Compares two integers for equality.
Parameters:

self : The first integer to compare.
other : The second integer to compare.
Returns true if both integers have the same value, false otherwise.
Example:
inspect(42 == 42, content="true")
inspect(42 == -42, content="false")
== Int
k {
          PatriciaTree::(key~ : Int, value~ : T) -> PatriciaTree[T]
Leaf(Int
key~, T
value=(T, T) -> T
combine(T
v, T
value))
        } else {
          fn[T] join(p0 : UInt, t0 : PatriciaTree[T], p1 : UInt, t1 : PatriciaTree[T]) -> PatriciaTree[T]
join(
            Int
k.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint(),
            (key~ : Int, value~ : T) -> PatriciaTree[T]
Leaf(Int
key=Int
k, T
value=T
v),
            Int
key.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint(),
            PatriciaTree[T]
tree,
          )
        }
      (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
BranchPatriciaTree[T]
(UInt
prefixPatriciaTree[T]
~, UInt
maskPatriciaTree[T]
~, PatriciaTree[T]
leftPatriciaTree[T]
~, PatriciaTree[T]
rightPatriciaTree[T]
~) as tree =>
        if fn match_prefix(key~ : UInt, prefix~ : UInt, mask~ : UInt) -> Bool
match_prefix(UInt
key=Int
k.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint(), UInt
prefix~, UInt
mask~) {
          if fn zero(k : UInt, mask~ : UInt) -> Bool
zero(Int
k.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint(), UInt
mask~) {
            PatriciaTree::(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix~, UInt
mask~, PatriciaTree[T]
left=(PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
left), PatriciaTree[T]
right~)
          } else {
            PatriciaTree::(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix~, UInt
mask~, PatriciaTree[T]
left~, PatriciaTree[T]
right=(PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
right))
          }
        } else {
          fn[T] join(p0 : UInt, t0 : PatriciaTree[T], p1 : UInt, t1 : PatriciaTree[T]) -> PatriciaTree[T]
join(Int
k.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint(), (key~ : Int, value~ : T) -> PatriciaTree[T]
Leaf(Int
key=Int
k, T
value=T
v), UInt
prefix, PatriciaTree[T]
tree)
        }
    }
  }

  (PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
self)
}

合并操作基本遵循相同的逻辑，略有不同的是它还要考虑前缀与掩码完全相同的情况。

///|
fn[T] enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree::fn[T] PatriciaTree::union_with(combine~ : (T, T) -> T, left : PatriciaTree[T], right : PatriciaTree[T]) -> PatriciaTree[T]
union_with(
  (T, T) -> T
combine~ : (type parameter T
T, type parameter T
T) -> type parameter T
T,
  PatriciaTree[T]
left : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T],
  PatriciaTree[T]
right : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T],
) -> enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T] {
  fn (PatriciaTree[T], PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
left : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T], PatriciaTree[T]
right : enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T]) -> enum PatriciaTree[T] {
  Empty
  Leaf(key~ : Int, value~ : T)
  Branch(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T])
}
PatriciaTree[type parameter T
T] {
    match (PatriciaTree[T]
left, PatriciaTree[T]
right) {
      (PatriciaTree[T]
Empty, PatriciaTree[T]
t) | (PatriciaTree[T]
t, PatriciaTree[T]
Empty) => PatriciaTree[T]
t
      ((key~ : Int, value~ : T) -> PatriciaTree[T]
Leaf(Int
key~, T
value~), PatriciaTree[T]
t) => PatriciaTree[T]
t.fn[T] PatriciaTree::insert_with(self : PatriciaTree[T], k : Int, v : T, combine~ : (T, T) -> T) -> PatriciaTree[T]
insert_with(Int
key, T
value, (T, T) -> T
combine~)
      (PatriciaTree[T]
t, (key~ : Int, value~ : T) -> PatriciaTree[T]
Leaf(Int
key~, T
value~)) =>
        PatriciaTree[T]
t.fn[T] PatriciaTree::insert_with(self : PatriciaTree[T], k : Int, v : T, combine~ : (T, T) -> T) -> PatriciaTree[T]
insert_with(Int
key, T
value, (T, T) -> T
combine=fn(T
x, T
y) { (T, T) -> T
combine(T
y, T
x) })
      (
        (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
BranchPatriciaTree[T]
(UInt
prefixPatriciaTree[T]
=UInt
pPatriciaTree[T]
, UInt
maskPatriciaTree[T]
=UInt
mPatriciaTree[T]
, PatriciaTree[T]
leftPatriciaTree[T]
=PatriciaTree[T]
s0PatriciaTree[T]
, PatriciaTree[T]
rightPatriciaTree[T]
=PatriciaTree[T]
s1PatriciaTree[T]
) as s,
        (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
BranchPatriciaTree[T]
(UInt
prefixPatriciaTree[T]
=UInt
qPatriciaTree[T]
, UInt
maskPatriciaTree[T]
=UInt
nPatriciaTree[T]
, PatriciaTree[T]
leftPatriciaTree[T]
=PatriciaTree[T]
t0PatriciaTree[T]
, PatriciaTree[T]
rightPatriciaTree[T]
=PatriciaTree[T]
t1PatriciaTree[T]
) as t,
      ) =>
        if UInt
m fn Eq::equal(self : UInt, other : UInt) -> Bool
Compares two unsigned 32-bit integers for equality.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand to compare with.
Returns true if both integers have the same value, false otherwise.
Example:
let a = 42U
let b = 42U
let c = 24U
inspect(a == b, content="true")
inspect(a == c, content="false")
== UInt
n (Bool, Bool) -> Bool
&& UInt
p fn Eq::equal(self : UInt, other : UInt) -> Bool
Compares two unsigned 32-bit integers for equality.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand to compare with.
Returns true if both integers have the same value, false otherwise.
Example:
let a = 42U
let b = 42U
let c = 24U
inspect(a == b, content="true")
inspect(a == c, content="false")
== UInt
q {
          // The trees have the same prefix. Merge the subtrees
          PatriciaTree::(prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(
            UInt
prefix=UInt
p,
            UInt
mask=UInt
m,
            PatriciaTree[T]
left=(PatriciaTree[T], PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
s0, PatriciaTree[T]
t0),
            PatriciaTree[T]
right=(PatriciaTree[T], PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
s1, PatriciaTree[T]
t1),
          )
        } else if UInt
m fn Compare::op_lt(x : UInt, y : UInt) -> Bool
< UInt
n (Bool, Bool) -> Bool
&& fn match_prefix(key~ : UInt, prefix~ : UInt, mask~ : UInt) -> Bool
match_prefix(UInt
key=UInt
q, UInt
prefix=UInt
p, UInt
mask=UInt
m) {
          // q contains p. Merge t with a subtree of s
          if fn zero(k : UInt, mask~ : UInt) -> Bool
zero(UInt
q, UInt
mask=UInt
m) {
            (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix=UInt
p, UInt
mask=UInt
m, PatriciaTree[T]
left=(PatriciaTree[T], PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
s0, PatriciaTree[T]
t), PatriciaTree[T]
right=PatriciaTree[T]
s1)
          } else {
            (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix=UInt
p, UInt
mask=UInt
m, PatriciaTree[T]
left=PatriciaTree[T]
s0, PatriciaTree[T]
right=(PatriciaTree[T], PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
s1, PatriciaTree[T]
t))
          }
        } else if UInt
m fn Compare::op_gt(x : UInt, y : UInt) -> Bool
> UInt
n (Bool, Bool) -> Bool
&& fn match_prefix(key~ : UInt, prefix~ : UInt, mask~ : UInt) -> Bool
match_prefix(UInt
key=UInt
p, UInt
prefix=UInt
q, UInt
mask=UInt
n) {
          // p contains q. Merge s with a subtree of t.
          if fn zero(k : UInt, mask~ : UInt) -> Bool
zero(UInt
p, UInt
mask=UInt
n) {
            (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix=UInt
q, UInt
mask=UInt
n, PatriciaTree[T]
left=(PatriciaTree[T], PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
s, PatriciaTree[T]
t0), PatriciaTree[T]
right=PatriciaTree[T]
t1)
          } else {
            (prefix~ : UInt, mask~ : UInt, left~ : PatriciaTree[T], right~ : PatriciaTree[T]) -> PatriciaTree[T]
Branch(UInt
prefix=UInt
q, UInt
mask=UInt
n, PatriciaTree[T]
left=PatriciaTree[T]
t0, PatriciaTree[T]
right=(PatriciaTree[T], PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
s, PatriciaTree[T]
t1))
          }
        } else {
          fn[T] join(p0 : UInt, t0 : PatriciaTree[T], p1 : UInt, t1 : PatriciaTree[T]) -> PatriciaTree[T]
join(UInt
p, PatriciaTree[T]
s, UInt
q, PatriciaTree[T]
t)
        }
    }
  }

  (PatriciaTree[T], PatriciaTree[T]) -> PatriciaTree[T]
go(PatriciaTree[T]
left, PatriciaTree[T]
right)
}

Big-endian Patricia Tree

Big-endian Patricia Tree在Patricia Tree的基础上将计算分支位的顺序改成了从最高位到最低位，

这样做有什么好处呢？

更好的局部性。在Big-endian Patricia Tree中，大小相近的整数键会被放在邻近的地方。
便于高效地按顺序遍历键，只要普通地实现前序/后序遍历即可。
常见情况下合并速度更快。在实践中，intmap里的整数键一般是连续的，这种情况下Big-endian Patricia Tree会有更长的公共前缀，让合并操作更快。
在Big-endian Patricia Tree中，如果把键看作无符号整数，右子树的每个键都大于当前节点的键(反过来，左子树是小于)。在编写查找函数时，只要使用无符号整数的比较就可判断接下来往哪个分支走，在大多数机器上这只需要一条指令即可完成，成本较低。

由于最终版本IntMap的实现与前文所述的Little Endian Patricia Tree相差不大，此处不再赘述，有需要的读者可以参考此仓库中的实现：https://github.com/moonbit-community/intmap

原实现中的一处错误

虽然IntMap的实现思路相当简洁明了，但在编写具体的实现代码时还是可能犯一些非常隐蔽的错误，甚至原论文作者在编写IntMap的SML实现时也未能幸免，后来又被OCaml的Ptset/Ptmap模块继承，直到2018年发表的QuickChecking Patricia Trees一文中这个问题才被发现。

具体来说，由于SML和OCaml语言没有提供无符号整数类型，在这两种语言的实现中IntMap类型里的掩码都通过int存储，但在union_with函数中对掩码进行比较时，他们都忘记了应该使用无符号整数的比较。

在 MoonBit 中实现 Shunting Yard 算法

2025年11月12日 · 阅读需 12 分钟

什么是 Shunting Yard 算法？

在编程语言或解释器的实现中，如何处理数学表达式一直是一个经典问题。我们希望能够像人一样理解“中缀表达式”（如 3 + 4 * 2），并正确考虑运算符优先级与括号。

1961 年，Edsger Dijkstra 提出了著名的 Shunting Yard 算法，它提供了一种机械化的方式来将中缀表达式转换为后缀表达式（RPN）或抽象语法树（AST）。算法的名字来源于铁路编组场：火车车厢通过在轨道之间来回调度实现排序，而在表达式处理中，我们通过两个栈来存储和调度操作数与操作符。想象一下你在脑子里计算 3 + 4 * 2 的过程：

你知道乘法优先级更高，所以要先算 4 * 2。
在此过程中，你会把前面的 3 和 + 临时“记在心里”。
等乘法结果出来，再把它和 3 相加。

Dijkstra 的洞见在于：这种人类计算时“临时记住某些东西再回来处理”的思维过程，其实可以用栈（stack）来模拟。就像铁路编组场会把火车车厢先临时停放在侧轨，再根据需要调度一样，算法通过把数字和运算符在不同的栈之间移动，来实现对运算顺序的控制。“Shunting Yard”（调度场算法）的名字正是来自这种铁路类比：

火车车厢通过在轨道间移动来完成排序；
数学表达式中的运算符和数字，也可以通过在栈之间移动来完成正确的排序与计算。

Dijkstra 把我们人类零散、混乱的计算过程，抽象成了一个清晰、机械化的流程，让计算机也能按照同样的逻辑来处理算式。

Shunting Yard 算法的基本流程

Shunting Yard 算法通过维护两个栈来保证表达式按照正确的优先级和结合性进行解析：

初始化

建立两个空栈：
- 运算符栈（op_stack），用于临时存放尚未处理的运算符和括号；
- 值栈（val_stack），用于存放操作数以及已经构造好的部分子表达式。
逐一扫描输入 token
- 若 token 为数字或变量：直接压入 val_stack。
- 若 token 为运算符：
  1. 检查 op_stack 栈顶元素。
  2. 当且仅当栈顶运算符的优先级高于当前运算符，或优先级相等且为左结合时，将该栈顶运算符弹出，并结合 val_stack 中的两个操作数，合成一个新的子表达式，再压回 val_stack。
  3. 重复此过程，直到不满足条件为止，然后将当前运算符压入 op_stack。
- 若 token 为左括号：压入 op_stack，作为分界标记。
- 若 token 为右括号：不断从 op_stack 弹出运算符，并用 val_stack 顶部的操作数组合成子表达式，直到遇到左括号为止；左括号本身丢弃，不会进入 val_stack。
清空运算符栈

当所有 token 扫描完成后，若 op_stack 中仍有运算符，则依次弹出，并与 val_stack 中的操作数组合成更大的表达式，直到运算符栈为空。
结束条件

最终，val_stack 中应只剩下一个元素，该元素即为完整的抽象语法树或后缀表达式。若栈内元素数量不为一，或存在未匹配的括号，则说明输入表达式存在错误。

演算示例

接下来我们以解析 (1 + 2) * (3 - 4) ^ 2 为例，来展示在读入 token 的过程中，两个栈是如何变化的，从而更好地理解 Shunting Yard 算法：

步骤	读入 token	运算符栈（op_stack）	值栈（val_stack）	说明
1	`(`	[`(`]	[]	左括号压入运算符栈
2	`1`	[`(`]	[`1`]	数字压入值栈
3	`+`	[`(`, `+`]	[`1`]	运算符压入运算符栈
4	`2`	[`(`, `+`]	[`1`, `2`]	数字压入值栈
5	`)`	[]	[`1 + 2`]	弹出直到左括号：`1` 与 `2` 结合为 `1+2`
6	`*`	[`*`]	[`1 + 2`]	运算符压入运算符栈
7	`(`	[`*`, `(`]	[`1 + 2`]	左括号压入运算符栈
8	`3`	[`*`, `(`]	[`1 + 2`, `3`]	数字压入值栈
9	`-`	[`*`, `(`, `-`]	[`1 + 2`, `3`]	运算符压入运算符栈
10	`4`	[`*`, `(`, `-`]	[`1 + 2`, `3`, `4`]	数字压入值栈
11	`)`	[`*`]	[`1 + 2`, `3 - 4`]	弹出直到左括号：`3` 与 `4` 结合为 `3-4`
12	`^`	[`*`, `^`]	[`1 + 2`, `3 - 4`]	幂运算符压入栈（右结合，不会触发弹出）
13	`2`	[`*`, `^`]	[`1 + 2`, `3 - 4`, `2`]	数字压入值栈
14	输入结束	[]	[`(1 + 2) * (3 - 4) ^ 2`]	清空运算符栈：先弹出 `^`，结合 `3-4` 与 `2`；再弹出 `*`，结合 `1+2` 与结果

在这个例子中，有以下几点值得注意：

括号优先处理在第一组括号 (1 + 2) 中，运算符 + 被延迟存放在运算符栈中，直到遇到右括号才与 1 和 2 结合。第二组括号 (3 - 4) 的处理过程完全相同。
优先级的体现当遇到 * 时，它被压入运算符栈。但随后遇到幂运算符 ^ 时，由于 ^ 的优先级高于 *，且是右结合，因此直接压栈，而不会触发 * 的弹出。
结合性的作用幂运算符 ^ 通常定义为右结合，这意味着表达式 a ^ b ^ c 会被解析为 a ^ (b ^ c)。在本例中，(3-4) ^ 2 保持这种结合方式，正确构建了子表达式。
最终结果在输入结束后，运算符栈依次被清空，最终形成完整的表达式：

(1 + 2) * ((3 - 4) ^ 2)

在 MoonBit 中实现 Shunting Yard 算法

首先我们需要定义表达式和 token 的类型：

enum Expr {
  (Int) -> Expr
Literal(Int
Int)
  (String, Expr, Expr) -> Expr
BinExpr(String
String, enum Expr {
  Literal(Int)
  BinExpr(String, Expr, Expr)
} derive(Show)
Expr, enum Expr {
  Literal(Int)
  BinExpr(String, Expr, Expr)
} derive(Show)
Expr)
} derive(trait Show {
  output(Self, &Logger) -> Unit
  to_string(Self) -> String
}
Trait for types that can be converted to String
Show)

enum Token {
  (Int) -> Token
Literal(Int
Int)
  (String) -> Token
Op(String
String)
  Token
LeftParen
  Token
RightParen
} derive(trait Show {
  output(Self, &Logger) -> Unit
  to_string(Self) -> String
}
Trait for types that can be converted to String
Show)

我们可以利用 MoonBit 中的正则表达式匹配语法，快速的实现一个简单的 tokenizer：

pub fn fn tokenize(input : StringView) -> Array[Token] raise
tokenize(StringView
input : type StringView
StringView) -> type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[enum Token {
  Literal(Int)
  Op(String)
  LeftParen
  RightParen
} derive(Show)
Token] raise {
  let Array[Unit]
tokens = []
  for StringView
str = StringView
input {
    lexmatch StringView
str {
      "[0-9]+" as n, rest => {
        tokens.push(Token::Literal(@strconv.parse_int(n)))
        continue rest
      }
      Unit
"[\-+*/^]" as o, rest => {
        tokens.push(Token::Op(o.to_string()))
        continue StringView
rest
      }
      "\(", rest => {
        tokens.push(Token::LeftParen)
        continue Unit
rest
      }
      "\)", rest => {
        tokens.push(Token::RightParen)
        continue rest
      }
      "[ \n\r\t]+", rest => continue rest
      "$", _ => break
      _ => fail("Invalid input")
    }
  }
  tokens
}

tokenize 函数的作用是把输入字符串分割成一系列 token：

匹配数字 [0-9]+，转换为 Token::Literal；
匹配四则运算符和幂运算符 [-+*/^]，转换为 Token::Op；
匹配括号 ( 与 )，分别转换为 LeftParen 和 RightParen；
匹配空格、换行等空白字符则直接跳过；
如果遇到不符合规则的字符，则报错。通过 lexmatch 和正则表达式，整个分词过程既简洁又高效。

接下来我们定义一个全局的操作符表，用于存储操作符的优先级和结合性：

priv enum Associativity {
  Associativity
Left
  Associativity
Right
}

priv struct OpInfo {
  Int
precedence : Int
Int
  Associativity
associativity : enum Associativity {
  Left
  Right
}
Associativity
}

let Map[String, OpInfo]
op_table : type Map[K, V]
Mutable linked hash map that maintains the order of insertion, not thread safe.
Example
  let map = { 3: "three", 8 :  "eight", 1 :  "one"}
  assert_eq(map.get(2), None)
  assert_eq(map.get(3), Some("three"))
  map.set(3, "updated")
  assert_eq(map.get(3), Some("updated"))
Map[String
String, struct OpInfo {
  precedence: Int
  associativity: Associativity
}
OpInfo] = {
  "+": { Int
precedence: 10, Associativity
associativity: Associativity
Left },
  "-": { Int
precedence: 10, Associativity
associativity: Associativity
Left },
  "*": { Int
precedence: 20, Associativity
associativity: Associativity
Left },
  "/": { Int
precedence: 20, Associativity
associativity: Associativity
Left },
  "^": { Int
precedence: 30, Associativity
associativity: Associativity
Right },
}

这里通过 op_table 定义了常见运算符的优先级与结合性：

+ 和 - 的优先级最低（10），是左结合；

* 和 / 的优先级更高（20），同样是左结合；
^（幂运算）的优先级最高（30），但它是右结合。

接下来我们定义一个辅助函数，用于判断在遇到一个新的运算符时，是否需要先处理（弹出）栈顶的运算符：

fn fn should_pop(top_op_info~ : OpInfo, incoming_op_info~ : OpInfo) -> Bool
should_pop(OpInfo
top_op_info~ : struct OpInfo {
  precedence: Int
  associativity: Associativity
}
OpInfo, OpInfo
incoming_op_info~ : struct OpInfo {
  precedence: Int
  associativity: Associativity
}
OpInfo) -> Bool
Bool {
  OpInfo
top_op_info.Int
precedence fn Compare::op_gt(x : Int, y : Int) -> Bool
> OpInfo
incoming_op_info.Int
precedence (Bool, Bool) -> Bool
||
  (
    OpInfo
top_op_info.Int
precedence fn Eq::equal(self : Int, other : Int) -> Bool
Compares two integers for equality.
Parameters:

self : The first integer to compare.
other : The second integer to compare.
Returns true if both integers have the same value, false otherwise.
Example:
inspect(42 == 42, content="true")
inspect(42 == -42, content="false")
== OpInfo
incoming_op_info.Int
precedence (Bool, Bool) -> Bool
&&
    OpInfo
top_op_info.Associativity
associativity is Associativity
Left
  )
}

should_pop 的逻辑是 Shunting Yard 算法的核心之一：

如果栈顶运算符的优先级高于新运算符，则应当先处理栈顶运算符；
如果两者优先级相等，并且栈顶运算符是左结合，同样应当先处理栈顶运算符；
否则，保留栈顶运算符，把新运算符直接压入栈。

接下来我们实现表达式的解析函数：

pub fn fn parse_expr(tokens : Array[Token]) -> Expr
parse_expr(Array[Token]
tokens : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[enum Token {
  Literal(Int)
  Op(String)
  LeftParen
  RightParen
} derive(Show)
Token]) -> enum Expr {
  Literal(Int)
  BinExpr(String, Expr, Expr)
} derive(Show)
Expr {
  let Array[String]
op_stack : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[String
String] = []
  let Array[Expr]
val_stack : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[enum Expr {
  Literal(Int)
  BinExpr(String, Expr, Expr)
} derive(Show)
Expr] = []
  fn (String) -> Unit
push_binary_expr(String
top_op) {
    let Expr
right = Array[Expr]
val_stack.fn[T] Array::pop(self : Array[T]) -> T?
Removes the last element from an array and returns it, or None if it is empty.
Example
  let v = [1, 2, 3]
  assert_eq(v.pop(), Some(3))
  assert_eq(v, [1, 2])
pop().fn[X] Option::unwrap(self : X?) -> X
Extract the value in Some.
If the value is None, it throws a panic.
unwrap()
    let Expr
left = Array[Expr]
val_stack.fn[T] Array::pop(self : Array[T]) -> T?
Removes the last element from an array and returns it, or None if it is empty.
Example
  let v = [1, 2, 3]
  assert_eq(v.pop(), Some(3))
  assert_eq(v, [1, 2])
pop().fn[X] Option::unwrap(self : X?) -> X
Extract the value in Some.
If the value is None, it throws a panic.
unwrap()
    Array[Expr]
val_stack.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(Expr::(String, Expr, Expr) -> Expr
BinExpr(String
top_op, Expr
left, Expr
right))
  }

  for Token
token in Array[Token]
tokens {
    match Token
token {
      (Int) -> Token
Literal(Int
n) => Array[Expr]
val_stack.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(Expr::(Int) -> Expr
Literal(Int
n))
      (String) -> Token
Op(String
incoming_op) => {
        let OpInfo
incoming_op_info = let op_table : Map[String, OpInfo]
op_tablefn[K : Hash + Eq, V] Map::op_get(self : Map[K, V], key : K) -> V
[incoming_op]
        while true {
          match Array[String]
op_stack.fn[A] Array::last(self : Array[A]) -> A?
Returns the last element of the array, or None if the array is empty.
Parameters:

array : The array to get the last element from.
Returns an optional value containing the last element of the array. The
result is None if the array is empty, or Some(x) where x is the last
element of the array.
Example:
let arr = [1, 2, 3]
inspect(arr.last(), content="Some(3)")
let empty : Array[Int] = []
inspect(empty.last(), content="None")
last() {
            String?
None => break
            (String) -> String?
Some(String
top_op) =>
              if String
top_op fn[T : Eq] @moonbitlang/core/builtin.op_notequal(x : T, y : T) -> Bool
!= "(" (Bool, Bool) -> Bool
&&
                fn should_pop(top_op_info~ : OpInfo, incoming_op_info~ : OpInfo) -> Bool
should_pop(OpInfo
top_op_info=let op_table : Map[String, OpInfo]
op_tablefn[K : Hash + Eq, V] Map::op_get(self : Map[K, V], key : K) -> V
[top_op], OpInfo
incoming_op_info~) {
                Array[String]
op_stack.fn[T] Array::pop(self : Array[T]) -> T?
Removes the last element from an array and returns it, or None if it is empty.
Example
  let v = [1, 2, 3]
  assert_eq(v.pop(), Some(3))
  assert_eq(v, [1, 2])
pop() |> fn[T] ignore(t : T) -> Unit
Evaluates an expression and discards its result. This is useful when you want
to execute an expression for its side effects but don't care about its return
value, or when you want to explicitly indicate that a value is intentionally
unused.
Parameters:

value : The value to be ignored. Can be of any type.
Example:
let x = 42
ignore(x) // Explicitly ignore the value
let mut sum = 0
ignore([1, 2, 3].iter().each(x => sum = sum + x)) // Ignore the Unit return value of each()
ignore
                (String) -> Unit
push_binary_expr(String
top_op)
              } else {
                break
              }
          }
        }
        Array[String]
op_stack.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(String
incoming_op)
      }
      Token
LeftParen => Array[String]
op_stack.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push("(")
      Token
RightParen =>
        while Array[String]
op_stack.fn[T] Array::pop(self : Array[T]) -> T?
Removes the last element from an array and returns it, or None if it is empty.
Example
  let v = [1, 2, 3]
  assert_eq(v.pop(), Some(3))
  assert_eq(v, [1, 2])
pop() is (String) -> String?
Some(String
top_op) {
          if String
top_op fn[T : Eq] @moonbitlang/core/builtin.op_notequal(x : T, y : T) -> Bool
!= "(" {
            (String) -> Unit
push_binary_expr(String
top_op)
          } else {
            break
          }
        }
    }
  }
  while Array[String]
op_stack.fn[T] Array::pop(self : Array[T]) -> T?
Removes the last element from an array and returns it, or None if it is empty.
Example
  let v = [1, 2, 3]
  assert_eq(v.pop(), Some(3))
  assert_eq(v, [1, 2])
pop() is (String) -> String?
Some(String
top_op) {
    (String) -> Unit
push_binary_expr(String
top_op)
  }
  Array[Expr]
val_stack.fn[T] Array::pop(self : Array[T]) -> T?
Removes the last element from an array and returns it, or None if it is empty.
Example
  let v = [1, 2, 3]
  assert_eq(v.pop(), Some(3))
  assert_eq(v, [1, 2])
pop().fn[X] Option::unwrap(self : X?) -> X
Extract the value in Some.
If the value is None, it throws a panic.
unwrap()
}

parse_expr 是整个 Shunting Yard 算法的核心实现：

数据结构准备
- op_stack 存储运算符和括号；
- val_stack 存储操作数或部分构造好的子表达式；
- 内部函数 push_binary_expr 封装了一个小步骤：从值栈中弹出两个操作数，结合运算符，生成一个新的 BinExpr 节点，并压回值栈。
遍历 token
- 数字：直接压入 val_stack。
- 运算符：不断检查 op_stack 栈顶的运算符，如果优先级更高或需要先计算，则弹出并构造子表达式；直到不满足条件时，把新运算符压入栈。
- 左括号：压入 op_stack，用于分隔子表达式。
- 右括号：持续弹出运算符，并结合值栈中的操作数形成子表达式，直到遇到匹配的左括号。
清空运算符栈

遍历完成后，可能仍有运算符滞留在 op_stack 中，这时需要逐一弹出，并结合值栈中的操作数，直到运算符栈为空。
返回结果

最终，值栈中应当只剩下一个元素，它就是完整的抽象语法树。若不是这种情况，说明输入表达式存在语法错误。

最后我们可以定义一个简单的 eval 函数，以便于进行测试：

pub fn fn eval(expr : Expr) -> Int
eval(Expr
expr : enum Expr {
  Literal(Int)
  BinExpr(String, Expr, Expr)
} derive(Show)
Expr) -> Int
Int {
  match Expr
expr {
    (Int) -> Expr
Literal(Int
n) => Int
n
    (String, Expr, Expr) -> Expr
BinExpr(String
op, Expr
left, Expr
right) =>
      match String
op {
        "+" => fn eval(expr : Expr) -> Int
eval(Expr
left) fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ fn eval(expr : Expr) -> Int
eval(Expr
right)
        "-" => fn eval(expr : Expr) -> Int
eval(Expr
left) fn Sub::sub(self : Int, other : Int) -> Int
Performs subtraction between two 32-bit integers, following standard two's
complement arithmetic rules. When the result overflows or underflows, it
wraps around within the 32-bit integer range.
Parameters:

self : The minuend (the number being subtracted from).
other : The subtrahend (the number to subtract).
Returns the difference between self and other.
Example:
let a = 42
let b = 10
inspect(a - b, content="32")
let max = 2147483647 // Int maximum value
inspect(max - -1, content="-2147483648") // Overflow case
- fn eval(expr : Expr) -> Int
eval(Expr
right)
        "*" => fn eval(expr : Expr) -> Int
eval(Expr
left) fn Mul::mul(self : Int, other : Int) -> Int
Multiplies two 32-bit integers. This is the implementation of the *
operator for Int.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns the product of the two integers. If the result overflows the range of
Int, it wraps around according to two's complement arithmetic.
Example:
inspect(42 * 2, content="84")
inspect(-10 * 3, content="-30")
let max = 2147483647 // Int.max_value
inspect(max * 2, content="-2") // Overflow wraps around
* fn eval(expr : Expr) -> Int
eval(Expr
right)
        "/" => fn eval(expr : Expr) -> Int
eval(Expr
left) fn Div::div(self : Int, other : Int) -> Int
Performs integer division between two 32-bit integers. The result is
truncated towards zero (rounds down for positive numbers and up for negative
numbers).
Parameters:

dividend : The first integer operand to be divided.
divisor : The second integer operand that divides the dividend.
Returns the quotient of the division operation.
Throws a panic if divisor is zero.
Example:
inspect(10 / 3, content="3") // truncates towards zero
inspect(-10 / 3, content="-3")
inspect(10 / -3, content="-3")
/ fn eval(expr : Expr) -> Int
eval(Expr
right)
        "^" => {
          fn (Int, Int) -> Int
pow(Int
base : Int
Int, Int
exp : Int
Int) -> Int
Int {
            if Int
exp fn Eq::equal(self : Int, other : Int) -> Bool
Compares two integers for equality.
Parameters:

self : The first integer to compare.
other : The second integer to compare.
Returns true if both integers have the same value, false otherwise.
Example:
inspect(42 == 42, content="true")
inspect(42 == -42, content="false")
== 0 {
              1
            } else {
              Int
base fn Mul::mul(self : Int, other : Int) -> Int
Multiplies two 32-bit integers. This is the implementation of the *
operator for Int.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns the product of the two integers. If the result overflows the range of
Int, it wraps around according to two's complement arithmetic.
Example:
inspect(42 * 2, content="84")
inspect(-10 * 3, content="-30")
let max = 2147483647 // Int.max_value
inspect(max * 2, content="-2") // Overflow wraps around
* (Int, Int) -> Int
pow(Int
base, Int
exp fn Sub::sub(self : Int, other : Int) -> Int
Performs subtraction between two 32-bit integers, following standard two's
complement arithmetic rules. When the result overflows or underflows, it
wraps around within the 32-bit integer range.
Parameters:

self : The minuend (the number being subtracted from).
other : The subtrahend (the number to subtract).
Returns the difference between self and other.
Example:
let a = 42
let b = 10
inspect(a - b, content="32")
let max = 2147483647 // Int maximum value
inspect(max - -1, content="-2147483648") // Overflow case
- 1)
            }
          }

          (Int, Int) -> Int
pow(fn eval(expr : Expr) -> Int
eval(Expr
left), fn eval(expr : Expr) -> Int
eval(Expr
right))
        }
        _ => fn[T] abort(string : String, loc~ : SourceLoc = _) -> T
abort("Invalid operator")
      }
  }
}

///|
pub fn fn parse_and_eval(input : String) -> Int raise
parse_and_eval(String
input : String
String) -> Int
Int raise {
  fn eval(expr : Expr) -> Int
eval(fn parse_expr(tokens : Array[Token]) -> Expr
parse_expr(fn tokenize(input : StringView) -> Array[Token] raise
tokenize(String
input)))
}

并通过一些简单的测试用例来验证我们的实现：

test "parse_and_eval" {
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("1 + 2 * 3"), String
content="7")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("2 ^ 3 ^ 2"), String
content="512")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("(2 ^ 3) ^ 2"), String
content="64")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("(1 + 2) * 3"), String
content="9")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("10 - (3 + 2)"), String
content="5")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("2 * (3 + 4)"), String
content="14")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("(5 + 3) / 2"), String
content="4")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("10 / 2 - 1"), String
content="4")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("1 + 2 + 3"), String
content="6")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("10 - 5 - 2"), String
content="3")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("5"), String
content="5")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("(1 + 2) * (3 + 4)"), String
content="21")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("2 ^ (1 + 2)"), String
content="8")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("1 + 2 * 3 - 4 / 2 + 5"), String
content="10")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("((1 + 2) * 3) ^ 2 - 10"), String
content="71")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("100 / (2 * 5) + 3 * (4 - 1)"), String
content="19")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("2 ^ 2 * 3 + 1"), String
content="13")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn parse_and_eval(input : String) -> Int raise
parse_and_eval("1 + 2 * 3 ^ 2 - 4 / 2"), String
content="17")
}

小结

Shunting Yard 算法的核心思想在于使用两个栈来显式管理运算过程：

值栈（val_stack）用于保存数字和已经组合好的部分子表达式；
运算符栈（op_stack）用于保存尚未处理的运算符和括号。

通过定义运算符的优先级与结合性，并在扫描 token 的过程中不断比较和弹出栈顶运算符，Shunting Yard 能够保证表达式被按照正确的顺序组合成抽象语法树（AST）。最终，当所有 token 被读取并且运算符栈清空后，值栈中剩下的就是完整的表达式树。

这种方法直观地模拟了我们手工计算时的思路：先把暂时不能计算的内容“记下来”，等条件合适时再取出处理。它的流程清晰、实现简洁，非常适合作为学习表达式解析的起点。

之前 MoonBit Pearl 中发布过一篇介绍 Pratt parsing 的文章，两者都是解决“如何正确解析表达式优先级和结合性”的经典方法，但它们的思路截然不同。 Shunting Yard 使用循环和显式的数据结构，通过运算符栈和值栈来管理尚未处理的符号和部分子表达式，整个过程像是手工操纵两个栈，逻辑清晰且容易跟踪。Pratt Parser 则基于递归下降，每个 token 定义在不同上下文下的解析方式，解析的推进依赖语言运行时的调用栈：每一次递归调用都相当于把尚未完成的状态压入栈中，返回时再继续组合。换句话说，Pratt Parser 将“栈”的存在隐藏在递归调用里，而 Shunting Yard 则把这种状态管理显式化，用循环和数据结构来直接模拟出来。因此，可以认为 Shunting Yard 是将 Pratt Parser 中隐含在调用栈里的机制转写为显式的栈操作。前者步骤机械化，适合快速实现固定的运算符解析；后者更灵活，尤其在处理前缀、后缀或自定义运算符时更为自然。

使用 MoonBit 和 Wassette 构建安全的 WebAssembly 工具

2025年11月5日 · 阅读需 9 分钟

欢迎来到 MoonBit 和 Wassette 的世界！本教程将带您一步步构建一个基于 WebAssembly 组件模型的安全工具。通过一个实用的天气查询应用示例，您将学习如何利用 MoonBit 的高效性和 wassette 的安全特性，创建功能强大的 AI 工具。

wassette 和 MCP 简介

MCP（Model Completion Protocol）是 AI 模型与外部工具交互的协议。当 AI 需要执行特定任务（如网络访问或数据查询）时，会通过 MCP 调用相应工具。这种机制扩展了 AI 的能力，但也带来安全挑战。

wassette 是微软开发的一个基于 WebAssembly 组件模型的运行时，为 AI 系统提供安全执行外部工具的环境。它通过沙箱隔离和精确的权限控制，解决了 AI 工具可能带来的安全风险。

wassette 让工具运行在隔离环境中，权限受策略文件严格限制，接口通过 WIT（WebAssembly Interface Type）清晰定义。同时，也利用 WIT 接口来生成工具交互的数据格式。

总体流程

在开始之前，让我们先了解一下整体流程：

让我们开始这段奇妙的旅程吧！

第1步：安装必要工具

首先，我们需要安装三个工具（我们假设已经安装 MoonBit 工具链）：

wasm-tools：WebAssembly 工具集，用于处理和操作 Wasm 文件
wit-deps：WebAssembly 接口类型依赖管理器
wit-bindgen：WebAssembly 接口类型绑定生成器，用于生成语言绑定
wassette：基于 Wasm 组件模型的运行时，用于执行我们的工具

其中，wasm-tools wit-deps wit-bindgen 可通过 cargo 安装（需安装 Rust）：

cargo install wasm-tools
cargo install wit-deps-cli
cargo install wit-bindgen-cli

或从 GitHub Release 下载：

wit-bindgen: https://github.com/bytecodealliance/wit-bindgen/releases/tag/v0.45.0
wasm-tools: https://github.com/bytecodealliance/wasm-tools/releases/tag/v1.238.0
wit-deps: https://github.com/bytecodealliance/wit-deps/releases/tag/v0.5.0

wassette 需从 GitHub Release 下载：

wassette: https://github.com/microsoft/wassette/releases/tag/v0.3.4

第2步：定义接口

接口定义是整个工作流程的核心。我们使用 WebAssembly 接口类型 (WIT) 格式来定义组件的接口。

mkdir -p weather-app/wit
cd weather-app

创建 wit/deps.toml

在 wit 目录下创建 deps.toml 文件，定义项目依赖：

cli = "https://github.com/WebAssembly/wasi-cli/archive/refs/tags/v0.2.7.tar.gz"
http = "https://github.com/WebAssembly/wasi-http/archive/refs/tags/v0.2.7.tar.gz"

这些依赖项指定了我们将使用的 WASI（WebAssembly 系统接口）组件：

cli：提供命令行接口功能。在这个例子中未使用。
http：提供 HTTP 客户端和服务器功能。在这个例子中使用客户端功能。

然后，运行 wit-deps update。这个命令会获取依赖，并在 wit/deps/ 目录下展开。

创建 wit/world.wit

接下来，创建 wit/world.wit 文件来定义我们的组件接口。 WIT 是一种声明式接口描述语言，专为 WebAssembly 组件模型设计。它允许我们定义组件之间如何交互，而不需要关心具体的实现细节。具体详情可以查看组件模型手册。

package peter-jerry-ye:weather@0.1.0;

world w {
  import wasi:http/outgoing-handler@0.2.7;
  export get-weather: func(city: string) -> result<string, string>;
}

这个 WIT 文件定义了：

一个名为 peter-jerry-ye:weather 的包，版本为 0.1.0
一个名为 w 的世界（world），它是组件的主要接口
导入 WASI HTTP 的对外请求接口
导出一个名为 get-weather 的函数，它接受一个城市名称字符串，返回一个结果（成功时为天气信息字符串，失败时为错误信息字符串）

第3步：生成代码

现在我们已经定义了接口，下一步是生成相应的代码骨架。我们使用 wit-bindgen 工具来为 MoonBit 生成绑定代码：

# 确保您在项目根目录下
wit-bindgen moonbit --derive-eq --derive-show --derive-error wit

这个命令会读取 wit 目录中的文件，并生成相应的 MoonBit 代码。生成的文件将放在 gen 目录下。

注：当前生成版本存在部分警告，之后会进行修复。

生成的目录结构应该如下：

.
├── ffi/
├── gen/
│   ├── ffi.mbt
│   ├── moon.pkg.json
│   ├── world
│   │   └── w
│   │       ├── moon.pkg.json
│   │       └── stub.mbt
│   └── world_w_export.mbt
├── interface/
├── moon.mod.json
├── Tutorial.md
├── wit/
└── world/

这些生成的文件包含了：

基础的 FFI（外部函数接口）代码（ffi/）
生成的导入函数（world/ interface/
导出函数的包装器（gen/）
待实现的 stub.mbt 文件

第4步：修改生成的代码

现在我们需要修改生成的存根文件，实现我们的天气查询功能。主要需要编辑的是 gen/world/w/stub.mbt 文件以及同目录下的 moon.pkg.json。在此之前，先让我们添加一下依赖，方便后续实现：

moon update
moon add moonbitlang/x

{
  "import": [
    "peter-jerry-ye/weather/interface/wasi/http/types",
    "peter-jerry-ye/weather/interface/wasi/http/outgoingHandler",
    "peter-jerry-ye/weather/interface/wasi/io/poll",
    "peter-jerry-ye/weather/interface/wasi/io/streams",
    "peter-jerry-ye/weather/interface/wasi/io/error",
    "moonbitlang/x/encoding"
  ]
}

让我们看一下生成的存根代码：

// Generated by `wit-bindgen` 0.44.0.

///|
pub fn fn get_weather(city : String) -> Result[String, String]
get_weather(String
city : String
String) -> enum Result[A, B] {
  Err(B)
  Ok(A)
}
Result[String
String, String
String] {
  ... // 这里是我们需要实现的部分
}

现在，我们需要添加实现代码，使用 HTTP 客户端请求天气信息。编辑 gen/world/w/stub.mbt 文件，编辑如下：

///|
pub fn fn get_weather(city : String) -> Result[String, String]
get_weather(String
city : String
String) -> enum Result[A, B] {
  Err(B)
  Ok(A)
}
Result[String
String, String
String] {
  (try? fn get_weather_(city : String) -> String raise
利用 MoonBit 错误处理机制，简化实现
get_weather_(String
city)).fn[T, E, F] Result::map_err(self : Result[T, E], f : (E) -> F) -> Result[T, F]
Maps the value of a Result if it is Err into another, otherwise returns the Ok value unchanged.
Example
  let x: Result[Int, String] = Err("error")
  let y = x.map_err((v : String) => { v + "!" })
  assert_eq(y, Err("error!"))
map_err(_.fn[Self : Show] Show::to_string(self : Self) -> String
Default implementation for Show::to_string, uses a StringBuilder
to_string())
}

///| 利用 MoonBit 错误处理机制，简化实现
fn fn get_weather_(city : String) -> String raise
利用 MoonBit 错误处理机制，简化实现
get_weather_(String
city : String
String) -> String
String raise {
  // 创建请求
  let Unit
request = (Unit) -> Unit
@types.OutgoingRequest::(Unit) -> Unit
outgoing_request(
    () -> Unit
@types.Fields::() -> Unit
fields(),
  )
  // 为了天气，我们访问 wttr.in 来获取
  if Unit
request.(Unit) -> Unit
set_authority(Unit
Some("wttr.in")) is (_/0) -> Unit
Err(_) {
    fn[T] fail(msg : String, loc~ : SourceLoc = _) -> T raise Failure
Raises a Failure error with a given message and source location.
Parameters:

message : A string containing the error message to be included in the
failure.
location : The source code location where the failure occurred.
Automatically provided by the compiler when not specified.
Returns a value of type T wrapped in a Failure error type.
Throws an error of type Failure with a message that includes both the
source location and the provided error message.
fail("Invalid Authority")
  }
  // 我们采用最简单的格式
  if Unit
request.(Unit) -> Unit
set_path_with_query(Unit
Some("/\{String
city}?format=3")) is (_/0) -> Unit
Err(_) {
    fn[T] fail(msg : String, loc~ : SourceLoc = _) -> T raise Failure
Raises a Failure error with a given message and source location.
Parameters:

message : A string containing the error message to be included in the
failure.
location : The source code location where the failure occurred.
Automatically provided by the compiler when not specified.
Returns a value of type T wrapped in a Failure error type.
Throws an error of type Failure with a message that includes both the
source location and the provided error message.
fail("Invalid path with query")
  }
  if Unit
request.(Unit) -> Unit
set_method(Unit
Get) is (_/0) -> Unit
Err(_) {
    fn[T] fail(msg : String, loc~ : SourceLoc = _) -> T raise Failure
Raises a Failure error with a given message and source location.
Parameters:

message : A string containing the error message to be included in the
failure.
location : The source code location where the failure occurred.
Automatically provided by the compiler when not specified.
Returns a value of type T wrapped in a Failure error type.
Throws an error of type Failure with a message that includes both the
source location and the provided error message.
fail("Invalid Method")
  }
  // 发出请求
  let Unit
future_response = (Unit, Unit) -> Unit
@outgoingHandler.handle(Unit
request, Unit
None).() -> Unit
unwrap_or_error()
  defer Unit
future_response.() -> Unit
drop()
  // 在这里，我们采用同步实现，等待请求返回
  let Unit
pollable = Unit
future_response.() -> Unit
subscribe()
  defer Unit
pollable.() -> Unit
drop()
  Unit
pollable.() -> Unit
block()
  // 在请求返回后，我们获取结果
  let Unit
response = Unit
future_response.() -> Unit
get().() -> Unit
unwrap().() -> Unit
unwrap().() -> Unit
unwrap_or_error()
  defer Unit
response.() -> Unit
drop()
  let Unit
body = Unit
response.() -> Unit
consume().() -> Unit
unwrap()
  defer Unit
body.() -> Unit
drop()
  let Unit
stream = Unit
body.() -> Unit
stream().() -> Unit
unwrap()
  defer Unit
stream.() -> Unit
drop()
  // 将数据流解码为字符串
  let Unit
decoder = (Unit) -> Unit
@encoding.decoder(Unit
UTF8)
  let StringBuilder
builder = type StringBuilder
StringBuilder::fn StringBuilder::new(size_hint? : Int) -> StringBuilder
Creates a new string builder with an optional initial capacity hint.
Parameters:

size_hint : An optional initial capacity hint for the internal buffer. If
less than 1, a minimum capacity of 1 is used. Defaults to 0. It is the size of bytes,
not the size of characters. size_hint may be ignored on some platforms, JS for example.
Returns a new StringBuilder instance with the specified initial capacity.
new()
  loop Unit
stream.(Int) -> Unit
blocking_read(1024) {
    (Unit) -> Unit
Ok(Unit
bytes) => {
      Unit
decoder.(Unit, StringBuilder, Bool) -> Unit
decode_to(
        Unit
bytes.() -> Unit
unsafe_reinterpret_as_bytes()[:],
        StringBuilder
builder,
        Bool
stream=true,
      )
      continue Unit
stream.(Int) -> Unit
blocking_read(1024)
    }
    // 如果流被关闭，则视为 EOF，正常结束
    (_/0) -> Unit
Err(_/0
Closed) => Unit
decoder.(String, StringBuilder, Bool) -> Unit
decode_to("", StringBuilder
builder, Bool
stream=false)
    // 如果出错，我们获取错误信息
    (_/0) -> Unit
Err((Unit) -> _/0
LastOperationFailed(Unit
e)) => {
      defer Unit
e.() -> Unit
drop()
      fn[T] fail(msg : String, loc~ : SourceLoc = _) -> T raise Failure
Raises a Failure error with a given message and source location.
Parameters:

message : A string containing the error message to be included in the
failure.
location : The source code location where the failure occurred.
Automatically provided by the compiler when not specified.
Returns a value of type T wrapped in a Failure error type.
Throws an error of type Failure with a message that includes both the
source location and the provided error message.
fail(Unit
e.() -> String
to_debug_string())
    }
  }
  StringBuilder
builder.fn StringBuilder::to_string(self : StringBuilder) -> String
Returns the current content of the StringBuilder as a string.
to_string()
}

这段代码实现了以下功能：

创建一个 HTTP 请求，目标是 wttr.in 天气服务
设置请求路径，包含城市名称和格式参数
发送请求并等待响应
从响应中提取内容
解码内容并返回天气信息字符串

这段代码使用了 WASI HTTP 接口来发送请求，以同步 API 进行交互。其中，defer 关键字确保资源在使用后被正确释放。

第5步：构建项目

现在我们已经实现了功能，下一步是构建项目。

# 编译 MoonBit 代码，生成核心 WebAssembly 模块
moon build --target wasm
# 嵌入 WIT 接口信息，指定字符串编码
wasm-tools component embed wit target/wasm/release/build/gen/gen.wasm -o core.wasm --encoding utf16
# 将核心 Wasm 模块转化为 Wasm 组件模块
wasm-tools component new core.wasm -o weather.wasm

构建成功后，会在项目根目录生成 weather.wasm 文件，这就是我们的 WebAssembly 组件。

之后，我们将它加载到 wassette 的路径中。当然，也可以选择通过对话，让 AI 来进行动态加载，不仅可以加载本地文件，也可以加载远程服务器上的文件。

wassette component load file://$(pwd)/weather.wasm

第6步（可选）：配置安全策略

wassette 会严格控制 WebAssembly 组件的权限，这是确保工具安全性的关键部分。这也是构建安全 MCP 工具的核心环节，通过细粒度的权限控制，我们可以确保工具只能执行预期的操作。

AI 可以在运行时通过调用默认的 wassette 的工具来进行赋权。我们可以预先执行这些命令。在我们的例子中，我们希望它能够访问 wttr.in 这个网站。因此，我们可以运行如下指令：

wassette permission grant network weather wttr.in

第7步：与 AI 交互

最后，我们可以使用 wassette 运行我们的组件，并与 AI 交互。以 VSCode Copilot 为例，我们修改 .vscode/mcp.json，添加服务器：

{
  "servers": {
    "wassette": {
      // 假设 wassette 被添加至路径中
      // 否则请填写 wassette 可执行文件所在路径
      "command": "wassette",
      "args": [
        "serve",
        // 我们在这里禁用动态加载以及动态授权等功能
        "--disable-builtin-tools",
        "--stdio"
      ],
      "type": "stdio"
    }
  },
  "inputs": []
}

在刷新重启 wassette 后，我们便可以询问 AI 当前某个城市的天气。

当然，如果我们允许使用动态加载功能，我们也可以和 AI 这么说：

用 wassette，加载组件 ./weather.wasm（注意使用 file schema），并查询深圳的天气

于是，AI 便会先后调用 load-component 以及 get-weather 两个工具，获取天气，并且给出最后回答：

组件已成功加载，深圳的天气是：☀️ +30°C。

总结

到这里，我们成功创建了一个基于 WebAssembly 组件模型的安全 MCP 工具，它可以：

通过定义清晰的接口
利用 MoonBit 的高效性
在 wassette 的安全沙箱中运行
与 AI 进行交互

Wassette 目前还只是 0.3.4 的版本，还缺少 MCP 的很多概念，如提示词、工作区、反向获取用户指令和 AI 生成能力等。但是它向我们展示了一个快速通过 Wasm 组件模型构建 MCP 的例子。

MoonBit 将会持续优化对于组件模型的能力，包括添加即将到来的 WASIp3 中异步的能力，并简化开发流程。敬请期待！

哈希表避坑指南

2025年10月29日 · 阅读需 16 分钟

Rynco Maekawa

本文介绍了哈希表的结构，演示了哈希表所面临的一个常见攻击手段——哈希洪泛攻击（hash flooding），以及如何在实践中消除这一攻击。

谁不喜欢哈希表呢？

它能以快如闪电的平均 $O(1)$ 访问速度^* 联系键值对，而你只需要提供两样东西：一个比较相等的函数和一个哈希函数，就这么简单。这一独特的性质使得哈希表在效率上常常优于其他关联性数据结构（如搜索树）。因此，哈希表现已成为编程语言中使用最广泛的数据结构之一。

从 Python 中平平无奇的 dict，到数据库和分布式系统，再到 JavaScript 对象，哈希表无处不在。它们支撑着数据库的索引系统，实现了高效的缓存机制，并构成了 Web 框架请求路由的骨干。现代编译器用它们来管理符号表，操作系统靠它们来进行进程管理，几乎每一个 Web 应用都用它们来维护用户状态。

无论你是在构建 Web 服务器、解析 JSON，还是在处理配置文件，亦或只是统计词频，你都很可能会用到哈希表。它们已经变得如此基础，以至于许多开发者都将它们 $O(1)$ 的魔法视为理所当然—— 但你有没有想过，这个 $O(1)$ 的理所当然^*到底是什么呢？

哈希表的内部构造

一个哈希表由两部分组成：一个桶数组和一个哈希函数。

struct MyHashMap[K, V] {
  Array[ChainingBucket[K, V]]
buckets : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[struct ChainingBucket[K, V] {
  values: Array[(K, V)]
}
Bucket[type parameter K
K, type parameter V
V]]
  (K) -> UInt
hash_fn : (type parameter K
K) -> UInt
UInt
}

桶数组包含了一系列所谓的"桶"。每个桶都存储着我们插入的一些数据。

哈希函数 H 会为每个键（key）关联一个整数。这个整数被用来在桶数组中寻找一个索引位置，以存储我们的值。这个索引通常是通过将该整数与桶数组的大小进行取模运算得出的，即 index = H(key) % bucket_array_size。哈希表期望这个函数满足两个重要性质：

相同的键总是被转换成相同的数字。即，若 a == b，则 H(a) == H(b)。

这个性质确保了，我们用某个键存入数据后，下次还能用同一个键准确地找到原来的位置。
对于不同的键，哈希函数产生的结果会尽可能均匀地分布在所有可能的结果空间中。

这个性质确保了不同的键会大概率被转换到不同的整数值，因此不太可能被映射到同一个桶中，从而保证了检索的效率。

现在你可能会问，如果两个键被映射到了同一个桶，会发生什么呢？那我们就不得不提哈希冲突了。

哈希冲突

当两个键的哈希值相同时，或者更广义地说，当两个键被映射到同一个桶时，就发生了哈希冲突。

由于哈希表的一切决策都基于哈希值（或桶索引），这两个键在哈希表看来就变得一模一样了—— 它们应该被放在同一个地方，但它们本身又并不相等，所以不能互相覆盖。

哈希表的设计者们有几种策略来处理冲突，这些策略大致可分为两类：

链地址法将这些冲突的键放在同一个桶里。现在，每个桶可能包含多个键的数据，而不仅仅是一个。当查找一个冲突的键时，需要遍历该桶中的所有键。

struct ChainingBucket[K, V] {
  Array[(K, V)]
values : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[(type parameter K
K, type parameter V
V)]
}

Java 的 HashMap 就是这种方法的一个著名例子。

开放地址法仍然坚持每个桶只放一个键，但当键发生冲突时，会使用一种独立的策略来选择另一个桶的索引。当查找一个键时，会按照这种策略的顺序进行搜索，直到可以确定没有更多可能的匹配项为止。
```
struct OpenAddressBucket[K, V] {
  Int
hash: Int
Int
  K
key: type parameter K
K
  V
value: type parameter V
V
}
```
MoonBit 标准库中的 Map 就是这种方法的一个例子。

无论哪种情况，当哈希冲突发生时，我们都别无选择，只能遍历我们找到的那个桶对应的所有键值对，来确定我们正在寻找的键是否存在。

为了简单起见，我们以一个使用链地址法的哈希表为例。哈希表的实现看起来大概是这样的：

typealias struct ChainingBucket[K, V] {
  values: Array[(K, V)]
}
ChainingBucket as Bucket

/// 搜索键存储的位置。
///
/// 返回 `(桶索引, 键在桶中的索引?, 完成的搜索次数)`
fn[K : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq, V] struct MyHashMap[K, V] {
  buckets: Array[ChainingBucket[K, V]]
  hash_fn: (K) -> UInt
}
MyHashMap::fn[K : Eq, V] MyHashMap::search(self : MyHashMap[K, V], key : K) -> (Int, Int?, Int)
搜索键存储的位置。
返回 (桶索引, 键在桶中的索引?, 完成的搜索次数)
search(MyHashMap[K, V]
self : struct MyHashMap[K, V] {
  buckets: Array[ChainingBucket[K, V]]
  hash_fn: (K) -> UInt
}
MyHashMap[type parameter K
K, type parameter V
V], K
key : type parameter K
K) -> (Int
Int, Int
Int?, Int
Int) {
  let UInt
hash = (MyHashMap[K, V]
self.(K) -> UInt
hash_fn)(K
key)
  let Int
bucket = (UInt
hash fn Mod::mod(self : UInt, other : UInt) -> UInt
Calculates the remainder of dividing one unsigned integer by another.
Parameters:

self : The unsigned integer dividend.
other : The unsigned integer divisor.
Returns the remainder of the division operation.
Throws a panic if other is zero.
Example:
let a = 17U
let b = 5U
inspect(a % b, content="2") // 17 divided by 5 gives quotient 3 and remainder 2
inspect(7U % 4U, content="3")
% MyHashMap[K, V]
self.Array[ChainingBucket[K, V]]
buckets.fn[T] Array::length(self : Array[T]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
let arr = [1, 2, 3]
inspect(arr.length(), content="3")
let empty : Array[Int] = []
inspect(empty.length(), content="0")
length().fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint()).fn UInt::reinterpret_as_int(self : UInt) -> Int
reinterpret the unsigned int as signed int
For number within the range of 0..=2^31-1,
the value is the same. For number within the range of 2^31..=2^32-1,
the value is negative
reinterpret_as_int()
  // 结果
  let mut Int?
found_index = Int?
None
  let mut Int
n_searches = 0
  // 遍历桶中所有的键值对。
  for Int
index, (K, V)
keyvalue in MyHashMap[K, V]
self.Array[ChainingBucket[K, V]]
bucketsfn[T] Array::op_get(self : Array[T], index : Int) -> T
Retrieves an element from the array at the specified index.
Parameters:

array : The array to get the element from.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Throws a panic if the index is negative or greater than or equal to the
length of the array.
Example:
let arr = [1, 2, 3]
inspect(arr[1], content="2")
[bucket].Array[(K, V)]
values {
    Int
n_searches fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+= 1
    if (K, V)
keyvalue.K
0 (_ : K, _ : K) -> Bool
== K
key { // 检查键是否匹配。
      Int?
found_index = (Int) -> Int?
Some(Int
index)
      break
    }
  }
  return (Int
bucket, Int?
found_index, Int
n_searches)
}

/// 插入一个新的键值对。
///
/// 返回完成的搜索次数。
fn[K : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq, V] struct MyHashMap[K, V] {
  buckets: Array[ChainingBucket[K, V]]
  hash_fn: (K) -> UInt
}
MyHashMap::fn[K : Eq, V] MyHashMap::insert(self : MyHashMap[K, V], key : K, value : V) -> Int
插入一个新的键值对。
返回完成的搜索次数。
insert(MyHashMap[K, V]
self : struct MyHashMap[K, V] {
  buckets: Array[ChainingBucket[K, V]]
  hash_fn: (K) -> UInt
}
MyHashMap[type parameter K
K, type parameter V
V], K
key : type parameter K
K, V
value : type parameter V
V) -> Int
Int {
  let (Int
bucket, Int?
index, Int
n_searches) = MyHashMap[K, V]
self.fn[K : Eq, V] MyHashMap::search(self : MyHashMap[K, V], key : K) -> (Int, Int?, Int)
搜索键存储的位置。
返回 (桶索引, 键在桶中的索引?, 完成的搜索次数)
search(K
key)
  if Int?
index is (Int) -> Int?
Some(Int
index) {
    MyHashMap[K, V]
self.Array[ChainingBucket[K, V]]
bucketsfn[T] Array::op_get(self : Array[T], index : Int) -> T
Retrieves an element from the array at the specified index.
Parameters:

array : The array to get the element from.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Throws a panic if the index is negative or greater than or equal to the
length of the array.
Example:
let arr = [1, 2, 3]
inspect(arr[1], content="2")
[bucket].Array[(K, V)]
valuesfn[T] Array::op_set(self : Array[T], index : Int, value : T) -> Unit
Sets the element at the specified index in the array to a new value. The
original value at that index is overwritten.
Parameters:

array : The array to modify.
index : The position in the array where the value will be set.
value : The new value to assign at the specified index.
Throws an error if index is negative or greater than or equal to the length
of the array.
Example:
let arr = [1, 2, 3]
arr[1] = 42
inspect(arr, content="[1, 42, 3]")
[index] = (K
key, V
value)
  } else {
    MyHashMap[K, V]
self.Array[ChainingBucket[K, V]]
bucketsfn[T] Array::op_get(self : Array[T], index : Int) -> T
Retrieves an element from the array at the specified index.
Parameters:

array : The array to get the element from.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Throws a panic if the index is negative or greater than or equal to the
length of the array.
Example:
let arr = [1, 2, 3]
inspect(arr[1], content="2")
[bucket].Array[(K, V)]
values.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push((K
key, V
value))
  }
  Int
n_searches
}

这就是 $O(1)$ 访问魔法背后所附带的条件—— 如果我们运气不好，就必须遍历所有东西。这使得哈希表在最坏情况下的复杂度变成了 $O(n)$ ，其中 $n$ 是哈希表中的键的数量。

制造一场冲突

对于我们用于哈希表的大多数哈希函数来说，这种冲突的最坏情况是很罕见的。这意味着我们通常不需要为最坏情况而烦恼，并且在绝大多数时间里都能享受到 $O(1)$ 的速度。

除非有人， ~~也许是某个心怀恶意的黑客，~~ 故意把你推入最坏情况。

一般来说，哈希函数都是确定性的，而且运算速度很快。所以，即使不去对函数本身进行高级的密码学分析，我们仍然可以通过暴力破解找到很多会相互冲突的键。¹

fn fn find_collision(bucket_count : Int, target_bucket : Int, n_collision_want : Int, hash_fn : (String) -> UInt) -> Array[String]
find_collision(
  Int
bucket_count : Int
Int,
  Int
target_bucket : Int
Int,
  Int
n_collision_want : Int
Int,
  (String) -> UInt
hash_fn : (String
String) -> UInt
UInt,
) -> type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[String
String] {
  let Array[String]
result = []
  let UInt
bucket_count = Int
bucket_count.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint()
  let UInt
target_bucket = Int
target_bucket.fn Int::reinterpret_as_uint(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint()
  for Int
i = 0; ; Int
i = Int
i fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ 1 {
    // 生成一些字符串键。
    let String
s = Int
i.fn Int::to_string(self : Int, radix~ : Int) -> String
Converts an integer to its string representation in the specified radix (base).
Example:
inspect((255).to_string(radix=16), content="ff")
inspect((-255).to_string(radix=16), content="-ff")
to_string(Int
radix=36)
    // 计算哈希值
    let UInt
hash = (String) -> UInt
hash_fn(String
s)
    let UInt
bucket_index = UInt
hash fn Mod::mod(self : UInt, other : UInt) -> UInt
Calculates the remainder of dividing one unsigned integer by another.
Parameters:

self : The unsigned integer dividend.
other : The unsigned integer divisor.
Returns the remainder of the division operation.
Throws a panic if other is zero.
Example:
let a = 17U
let b = 5U
inspect(a % b, content="2") // 17 divided by 5 gives quotient 3 and remainder 2
inspect(7U % 4U, content="3")
% UInt
bucket_count
    let UInt
bucket_index = if UInt
bucket_index fn Compare::op_lt(x : UInt, y : UInt) -> Bool
< 0 {
      UInt
bucket_index fn Add::add(self : UInt, other : UInt) -> UInt
Performs addition between two unsigned 32-bit integers. If the result
overflows, it wraps around according to the rules of modular arithmetic
(2^32).
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand to be added.
Returns the sum of the two unsigned integers, wrapped around if necessary.
Example:
let a = 42U
let b = 100U
inspect(a + b, content="142")

// Demonstrate overflow behavior
let max = 4294967295U // UInt::max_value
inspect(max + 1U, content="0")
+ UInt
bucket_count
    } else {
      UInt
bucket_index
    }
    // 检查它是否与我们的目标桶冲突。
    if UInt
bucket_index fn Eq::equal(self : UInt, other : UInt) -> Bool
Compares two unsigned 32-bit integers for equality.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand to compare with.
Returns true if both integers have the same value, false otherwise.
Example:
let a = 42U
let b = 42U
let c = 24U
inspect(a == b, content="true")
inspect(a == c, content="false")
== UInt
target_bucket {
      Array[String]
result.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(String
s)
      if Array[String]
result.fn[T] Array::length(self : Array[T]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
let arr = [1, 2, 3]
inspect(arr.length(), content="3")
let empty : Array[Int] = []
inspect(empty.length(), content="0")
length() fn Compare::op_ge(x : Int, y : Int) -> Bool
>= Int
n_collision_want {
        break
      }
    }
  }
  Array[String]
result
}

哈希洪泛攻击

手握这些会冲突的键，（扮演恶意黑客的）我们现在就可以攻击哈希表，持续利用其最坏情况下的复杂度。

考虑以下情况：你正在向同一个哈希表中插入键，但每个键都被映射到同一个桶中。每次插入时，哈希表都必须遍历桶中所有现有的键，以确定新键是否已经存在。

第一次插入与 0 个键比较，第二次与 1 个键比较，第三次与 2 个键比较，被比较的键的数量随着每次插入线性增长。对于 $n$ 次插入，被比较的键的总数是：

0 + 1 + \dots + (n - 1) = \frac{n(n - 1)}{2} = \frac{n^2 + n}{2}

这 $n$ 次插入操作总共需要 $O(n^2)$ 次比较才能完成²，而平均情况下只需要 $O(n)$ 次比较。这个操作将比它本应花费的时间长得多。

这种攻击不仅限于插入操作。每当一个被攻击的键被查找时，都会比较相同数量的键，因此每一个本应是 $O(1)$ 的操作现在都变成了 $O(n)$ 。这些原本耗时可以忽略不计的哈希表操作现在会变得极其缓慢，使得攻击者比以前更容易耗尽程序的资源。

这就是我们所说的哈希洪泛攻击（hash flooding attack），得名于它用冲突的键 “淹没” 了哈希表的同一个桶。

我们可以用我们之前写的哈希表实现来演示这一点：

/// 一个通过 Fowler-Noll-Vo 哈希函数实现的简单字符串哈希器。
/// https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
fn fn string_fnv_hash(s : String) -> UInt
一个通过 Fowler-Noll-Vo 哈希函数实现的简单字符串哈希器。
https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
string_fnv_hash(String
s : String
String) -> UInt
UInt {
  // 现实中应该直接在 s 背后的数组上工作，这里为了演示使用了 encode
  let Bytes
s_bytes = fn @moonbitlang/core/encoding/utf16.encode(str : StringView, bom? : Bool, endianness? : @encoding/utf16.Endian) -> Bytes
Encodes a string into a UTF-16 byte array.
Assuming the string is valid.
@encoding/utf16.encode(String
s)
  let mut UInt
acc : UInt
UInt = 0x811c9dc5
  for Byte
b in Bytes
s_bytes {
    UInt
acc = (UInt
acc fn BitXOr::lxor(self : UInt, other : UInt) -> UInt
Performs a bitwise XOR (exclusive OR) operation between two unsigned 32-bit
integers. Each bit in the result is set to 1 if the corresponding bits in the
operands are different, and 0 if they are the same.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns the result of the bitwise XOR operation.
Example:
let a = 0xFF00U // Binary: 1111_1111_0000_0000
let b = 0x0F0FU // Binary: 0000_1111_0000_1111
inspect(a ^ b, content="61455") // Binary: 1111_0000_0000_1111
^ Byte
b.fn Byte::to_uint(self : Byte) -> UInt
Converts a Byte to a UInt.
Parameters:

byte : The Byte value to be converted.
Returns the UInt representation of the Byte.
to_uint()) fn Mul::mul(self : UInt, other : UInt) -> UInt
Performs multiplication between two unsigned 32-bit integers. The result
wraps around if it exceeds the maximum value of UInt.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand.
Returns the product of the two unsigned integers. If the result exceeds the
maximum value of UInt (4294967295), it wraps around to the corresponding
value modulo 2^32.
Example:
let a = 3U
let b = 4U
inspect(a * b, content="12")
let max = 4294967295U
inspect(max * 2U, content="4294967294") // Wraps around to max * 2 % 2^32
* 0x01000193
  }
  UInt
acc
}

fn fn test_attack(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(
  Int
n_buckets : Int
Int,
  Array[String]
keys : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[String
String],
  (String) -> UInt
hash_fn : (String
String) -> UInt
UInt,
) -> Int
Int {
  let MyHashMap[String, Int]
map = { Array[ChainingBucket[String, Int]]
buckets: type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array::fn[T] Array::makei(length : Int, value : (Int) -> T raise?) -> Array[T] raise?
Creates a new array of the specified length, where each element is
initialized using an index-based initialization function.
Parameters:

length : The length of the new array. If length is less than or equal
to 0, returns an empty array.
initializer : A function that takes an index (starting from 0) and
returns a value of type T. This function is called for each index to
initialize the corresponding element.
Returns a new array of type Array[T] with the specified length, where each
element is initialized using the provided function.
Example:
let arr = Array::makei(3, i => i * 2)
inspect(arr, content="[0, 2, 4]")
makei(Int
n_buckets, _ => { Array[(String, Int)]
values: [] }), (String) -> UInt
hash_fn }
  let mut Int
total_searches = 0
  for String
key in Array[String]
keys {
    Int
total_searches fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+= MyHashMap[String, Int]
map.fn[K : Eq, V] MyHashMap::insert(self : MyHashMap[K, V], key : K, value : V) -> Int
插入一个新的键值对。
返回完成的搜索次数。
insert(String
key, 0)
  }
  Int
total_searches
}

test {
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("演示哈希洪泛攻击")
  let Int
bucket_count = 2048
  let Int
target_bucket_id = 42
  let Int
n_collision_want = 1000

  //
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("首先，尝试插入不冲突的键。")
  let Array[String]
non_colliding_keys = type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array::fn[T] Array::makei(length : Int, value : (Int) -> T raise?) -> Array[T] raise?
Creates a new array of the specified length, where each element is
initialized using an index-based initialization function.
Parameters:

length : The length of the new array. If length is less than or equal
to 0, returns an empty array.
initializer : A function that takes an index (starting from 0) and
returns a value of type T. This function is called for each index to
initialize the corresponding element.
Returns a new array of type Array[T] with the specified length, where each
element is initialized using the provided function.
Example:
let arr = Array::makei(3, i => i * 2)
inspect(arr, content="[0, 2, 4]")
makei(Int
n_collision_want,
    Int
i => (Int
i fn Mul::mul(self : Int, other : Int) -> Int
Multiplies two 32-bit integers. This is the implementation of the *
operator for Int.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns the product of the two integers. If the result overflows the range of
Int, it wraps around according to two's complement arithmetic.
Example:
inspect(42 * 2, content="84")
inspect(-10 * 3, content="-30")
let max = 2147483647 // Int.max_value
inspect(max * 2, content="-2") // Overflow wraps around
* 37).fn Int::to_string(self : Int, radix~ : Int) -> String
Converts an integer to its string representation in the specified radix (base).
Example:
inspect((255).to_string(radix=16), content="ff")
inspect((-255).to_string(radix=16), content="-ff")
to_string(Int
radix=36))
  let Int
n_compares_nc = fn test_attack(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(
    Int
bucket_count, Array[String]
non_colliding_keys, fn string_fnv_hash(s : String) -> UInt
一个通过 Fowler-Noll-Vo 哈希函数实现的简单字符串哈希器。
https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
string_fnv_hash,
  )
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "1000个不冲突键的总比较次数：\{Int
n_compares_nc}",
  )
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("")

  //
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("现在，我们希望所有键都冲突到 #\{Int
target_bucket_id} 号桶。")
  let Array[String]
colliding_keys = fn find_collision(bucket_count : Int, target_bucket : Int, n_collision_want : Int, hash_fn : (String) -> UInt) -> Array[String]
find_collision(
    Int
bucket_count, Int
target_bucket_id, Int
n_collision_want, fn string_fnv_hash(s : String) -> UInt
一个通过 Fowler-Noll-Vo 哈希函数实现的简单字符串哈希器。
https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
string_fnv_hash,
  )
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("找到了 \{Array[String]
colliding_keys.fn[T] Array::length(self : Array[T]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
let arr = [1, 2, 3]
inspect(arr.length(), content="3")
let empty : Array[Int] = []
inspect(empty.length(), content="0")
length()} 个冲突的键。")
  let Int
n_compares_c = fn test_attack(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(Int
bucket_count, Array[String]
colliding_keys, fn string_fnv_hash(s : String) -> UInt
一个通过 Fowler-Noll-Vo 哈希函数实现的简单字符串哈希器。
https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
string_fnv_hash)
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "1000个冲突键的总比较次数：\{Int
n_compares_c}",
  )

  //
  let Double
increase = Int
n_compares_c.fn Int::to_double(self : Int) -> Double
Converts a 32-bit integer to a double-precision floating-point number. The
conversion preserves the exact value since all integers in the range of Int
can be represented exactly as Double values.
Parameters:

self : The 32-bit integer to be converted.
Returns a double-precision floating-point number that represents the same
numerical value as the input integer.
Example:
let n = 42
inspect(n.to_double(), content="42")
let neg = -42
inspect(neg.to_double(), content="-42")
to_double() fn Div::div(self : Double, other : Double) -> Double
Performs division between two double-precision floating-point numbers.
Follows IEEE 754 standard for floating-point arithmetic, including handling
of special cases like division by zero (returns infinity) and operations
involving NaN.
Parameters:

self : The dividend (numerator) in the division operation.
other : The divisor (denominator) in the division operation.
Returns the result of dividing self by other. Special cases follow IEEE
754:

Division by zero returns positive or negative infinity based on the
dividend's sign
Operations involving NaN return NaN
Division of infinity by infinity returns NaN
Example:
inspect(6.0 / 2.0, content="3")
inspect(-6.0 / 2.0, content="-3")
inspect(1.0 / 0.0, content="Infinity")
/ Int
n_compares_nc.fn Int::to_double(self : Int) -> Double
Converts a 32-bit integer to a double-precision floating-point number. The
conversion preserves the exact value since all integers in the range of Int
can be represented exactly as Double values.
Parameters:

self : The 32-bit integer to be converted.
Returns a double-precision floating-point number that represents the same
numerical value as the input integer.
Example:
let n = 42
inspect(n.to_double(), content="42")
let neg = -42
inspect(neg.to_double(), content="-42")
to_double()
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("比较次数增加了 \{Double
increase} 倍")
}

上面代码的输出是：

演示哈希洪泛攻击
首先，尝试插入不冲突的键。
1000个不冲突键的总比较次数：347

现在，使用冲突的键...
找到了 1000 个冲突的键。
1000个冲突键的总比较次数：499500
比较次数增加了 1439.4812680115274 倍

……可以直接看到，现在的插入操作慢了大约 1000 倍！

在现实中，尽管哈希表中的桶数不像我们的例子那样是固定的，但它们通常遵循一定的增长序列，比如翻倍或遵循一个预定义的素数列表。这种增长模式使得桶的数量非常容易预测。因此，即使攻击者不知道确切的桶数，也能发起哈希洪泛攻击。

缓解哈希洪泛攻击

哈希洪泛攻击之所以能奏效，是因为攻击者确切地知道哈希函数是如何工作的，以及它是如何与键插入哈希表的位置相关联的。如果我们改变其中任何一个，攻击就不再有效了。

带"种子"的哈希函数

到目前为止，最简单的方法是防止攻击者确切地知道哈希算法是如何工作的。这听起来可能不可能，但哈希函数的性质实际上只需要在单个哈希表内部保持一致就行了！

在哈希表中，我们其实不需要一个可以在任何地方使用的、全局统一的"哈希值"，因为哈希表压根不在乎表以外洪水滔天，只要表本身保持一致就可以了。所以，只要简单地在不同的哈希表之间切换哈希函数，我们就能让攻击者无法预测其行为。

但你可能会说：“可现实世界中的哈希算法不是无限供应的啊！”

其实它可以是。还记得我们说哈希函数需要将值尽可能均匀地分布在结果空间中吗？这意味着，对于一个足够好的哈希函数，输入的微小变化会导致输出的巨大变化（被称为雪崩效应）。因此，为了给每个哈希表一个独一无二的哈希函数，我们只需要在输入我们想要哈希的数据之前，先给它 “喂” 一些该哈希表独有的数据。这被称为哈希函数的“种子"（seed）。这样，我们只要通过调整种子的值，就能获得无限供应的不同哈希函数了。

让我们用一个带种子的哈希函数和两个使用不同种子的哈希表来演示一下，哈希种子是如何解决这个问题的：

/// FNV 哈希的修改版，允许使用种子。
fn fn string_fnv_hash_seeded(seed : UInt) -> (String) -> UInt
FNV 哈希的修改版，允许使用种子。
string_fnv_hash_seeded(UInt
seed : UInt
UInt) -> (String
String) -> UInt
UInt {
  let Bytes
seed_bytes = UInt
seed.fn UInt::to_le_bytes(self : UInt) -> Bytes
Converts the UInt to a Bytes in little-endian byte order.
to_le_bytes()
  fn (String) -> UInt
string_fnv_hash(String
s : String
String) -> UInt
UInt {
    let Bytes
s_bytes = fn @moonbitlang/core/encoding/utf16.encode(str : StringView, bom? : Bool, endianness? : @encoding/utf16.Endian) -> Bytes
Encodes a string into a UTF-16 byte array.
Assuming the string is valid.
@encoding/utf16.encode(String
s)
    let mut UInt
acc : UInt
UInt = 0x811c9dc5
    // 混入种子字节。
    for Byte
b in Bytes
seed_bytes {
      UInt
acc = (UInt
acc fn BitXOr::lxor(self : UInt, other : UInt) -> UInt
Performs a bitwise XOR (exclusive OR) operation between two unsigned 32-bit
integers. Each bit in the result is set to 1 if the corresponding bits in the
operands are different, and 0 if they are the same.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns the result of the bitwise XOR operation.
Example:
let a = 0xFF00U // Binary: 1111_1111_0000_0000
let b = 0x0F0FU // Binary: 0000_1111_0000_1111
inspect(a ^ b, content="61455") // Binary: 1111_0000_0000_1111
^ Byte
b.fn Byte::to_uint(self : Byte) -> UInt
Converts a Byte to a UInt.
Parameters:

byte : The Byte value to be converted.
Returns the UInt representation of the Byte.
to_uint()) fn Mul::mul(self : UInt, other : UInt) -> UInt
Performs multiplication between two unsigned 32-bit integers. The result
wraps around if it exceeds the maximum value of UInt.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand.
Returns the product of the two unsigned integers. If the result exceeds the
maximum value of UInt (4294967295), it wraps around to the corresponding
value modulo 2^32.
Example:
let a = 3U
let b = 4U
inspect(a * b, content="12")
let max = 4294967295U
inspect(max * 2U, content="4294967294") // Wraps around to max * 2 % 2^32
* 0x01000193
    }
    // 哈希字符串字节。
    for Byte
b in Bytes
s_bytes {
      UInt
acc = (UInt
acc fn BitXOr::lxor(self : UInt, other : UInt) -> UInt
Performs a bitwise XOR (exclusive OR) operation between two unsigned 32-bit
integers. Each bit in the result is set to 1 if the corresponding bits in the
operands are different, and 0 if they are the same.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns the result of the bitwise XOR operation.
Example:
let a = 0xFF00U // Binary: 1111_1111_0000_0000
let b = 0x0F0FU // Binary: 0000_1111_0000_1111
inspect(a ^ b, content="61455") // Binary: 1111_0000_0000_1111
^ Byte
b.fn Byte::to_uint(self : Byte) -> UInt
Converts a Byte to a UInt.
Parameters:

byte : The Byte value to be converted.
Returns the UInt representation of the Byte.
to_uint()) fn Mul::mul(self : UInt, other : UInt) -> UInt
Performs multiplication between two unsigned 32-bit integers. The result
wraps around if it exceeds the maximum value of UInt.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand.
Returns the product of the two unsigned integers. If the result exceeds the
maximum value of UInt (4294967295), it wraps around to the corresponding
value modulo 2^32.
Example:
let a = 3U
let b = 4U
inspect(a * b, content="12")
let max = 4294967295U
inspect(max * 2U, content="4294967294") // Wraps around to max * 2 % 2^32
* 0x01000193
    }
    UInt
acc
  }

  (String) -> UInt
string_fnv_hash
}

test {
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("演示洪水攻击的缓解措施")
  let Int
bucket_count = 2048
  let Int
target_bucket_id = 42
  let Int
n_collision_want = 1000

  // 第一个表使用种子 42。
  let UInt
seed1 : UInt
UInt = 42
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("我们使用种子 \{UInt
seed1} 来寻找冲突")
  let (String) -> UInt
hash_fn1 = fn string_fnv_hash_seeded(seed : UInt) -> (String) -> UInt
FNV 哈希的修改版，允许使用种子。
string_fnv_hash_seeded(UInt
seed1)
  let Array[String]
colliding_keys = fn find_collision(bucket_count : Int, target_bucket : Int, n_collision_want : Int, hash_fn : (String) -> UInt) -> Array[String]
find_collision(
    Int
bucket_count, Int
target_bucket_id, Int
n_collision_want, (String) -> UInt
hash_fn1,
  )
  let Int
n_compares_c = fn test_attack(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(Int
bucket_count, Array[String]
colliding_keys, (String) -> UInt
hash_fn1)
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "使用种子 \{UInt
seed1} 时，1000个冲突键的总比较次数：\{Int
n_compares_c}",
  )
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("")

  // 第二个表使用不同的种子。这次我们用 100
  let UInt
seed2 : UInt
UInt = 100
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "现在我们为第二个表使用不同的种子，这次是 \{UInt
seed2}",
  )
  let (String) -> UInt
hash_fn2 = fn string_fnv_hash_seeded(seed : UInt) -> (String) -> UInt
FNV 哈希的修改版，允许使用种子。
string_fnv_hash_seeded(UInt
seed2)
  let Int
n_compares_nc = fn test_attack(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(Int
bucket_count, Array[String]
colliding_keys, (String) -> UInt
hash_fn2)
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "对于那些本应在种子 \{UInt
seed1} 下冲突的1000个键，现在的总比较次数：\{Int
n_compares_nc}",
  )
}

上面程序的输出是：

演示洪水攻击的缓解措施
我们使用种子 42 来寻找冲突
使用种子 42 时，1000个冲突键的总比较次数：499500

现在我们为第二个表使用不同的种子，这次是 100
对于那些本应在种子 42 下冲突的1000个键，现在的总比较次数：6342

我们可以看到，在第一个表中冲突的键，在第二个表中不再冲突了。³ 因此，我们通过这个简单的技巧成功地缓解了哈希洪泛攻击。

至于那个让每个哈希表随机化的种子从哪里来…… 对于能够访问外部随机源的程序（比如 Linux 的 /dev/urandom），使用它通常是最佳选择。对于无法访问这类源的程序（比如在 WebAssembly 沙箱中），在同一个进程中使用相同的种子、不同进程使用不同的种子也是一个方案（Python 就是这么做的）。甚至于，一个每次请求种子时就自增的简单计数器或许也已经足够了—— 对于攻击者来说，猜测已经创建过多少个哈希表仍然是比较困难的一件事。

其他选择

Java 使用了另一种解决方案，当太多的值占据同一个桶时，它会退而求其次，使用一棵二叉搜索树（红黑树）存储它们。是，这要求键除了可哈希之外，还必须是可比较的，但现在它保证了 $O(\log n)$ 的最坏情况复杂度，这总比 $O(n)$ 要好得多。

这为什么对我们很重要？

由于哈希表在程序中无处不在，在一个程序中找到一个你能控制其键的哈希表是极其容易的。尤其是在 Web 程序中每，请求头、Cookie、查询参数和 JSON 请求体都是键值对，并且通常存储在哈希表中，这可能使它们容易受到哈希洪泛攻击。

一个对程序有足够了解（编程语言、框架等）的恶意攻击者，可以尝试向 Web API 端点发送精心构造的请求负载。这些请求需要更长的时间来处理，所以如果一个常规的拒绝服务（DoS）攻击需要每秒 n 个请求才能使服务器瘫痪，那么哈希洪泛攻击可能只需要小一个数量级的攻击次数就能达到相同的效果。这使得它对攻击者来说效率高得多。这种攻击被称为 哈希拒绝服务（HashDoS） 攻击。

幸运的是，通过在哈希表中引入一些哪怕是轻微的不可预测模式（例如每个进程的随机性或带密钥的哈希），我们就可以使这类攻击变得异常困难，以至于对攻击者不再可行。此外，由于这种攻击高度依赖于对目标应用的语言、框架、架构和实现的了解，构造一个攻击本身就已经相当困难了，而现代的、配置良好的系统则更难被利用。

总结

哈希表为我们提供了强大的、平均时间复杂度为常数的访问方式—— 然而，这个"常数"的成立，是建立在一些假设之上的，而这些假设有时会被攻击者打破。一次有针对性的哈希洪泛攻击会迫使许多键进入同一个桶，将 $O(1)$ 的操作变成 $O(n)$ ，能非常高效地耗尽系统资源。

好消息是，缓解措施既简单又实用：为你的哈希表引入一些不可预测性，当仅靠哈希还不够时使用旁路信息，或者当行为看起来不对劲时重新哈希。有了这些，我们就可以让我们的哈希表既快速又安全。

顺便提一下，这也类似于比特币挖矿的工作原理：找到一个值添加到现有字符串中，使得整个内容的哈希值（逐位倒过来之后）模除某个给定值之后的结果等于零。 ↩
甚至有一个 Tumblr 博客专门记录编程语言中意料之外的二次方复杂度，叫做 Accidentally Quadratic。你甚至可以在这里找到一个与哈希表相关的例子——这个例子几乎算是一次手动引入的哈希洪泛攻击了。 ↩
你可能会注意到，这个数字仍然比我们用随机生成的不冲突键得到的数字要高一些。这可能与 FNV 哈希函数的设计并非追求最高质量的输出有关。由于两个种子非常接近，结果可能仍然存在一些相似性。使用一个更好的哈希函数（甚至是像 SipHash 这样的加密安全哈希函数）会大大减少这种影响。 ↩

使用 MoonBit 开发一个 HTTP 文件服务器

2025年10月22日 · 阅读需 17 分钟

在这篇文章中，我将会介绍如何使用 MoonBit 的异步编程功能和 moonbitlang/async 库，编写一个简单的 HTTP 文件服务器。如果你之前接触过 Python 语言，那么你可能知道，Python 有一个非常方便的内建 HTTP 服务器模块。只需要运行 python -m http.server，就能在当期文件夹启动一个文件服务器，用于局域网文件共享等用途。在这篇文章中，我们将用 MoonBit 实现一个类似功能的程序，并借此了解 MoonBit 的异步编程支持。我们还将额外支持一个 python -m http.server 没有的实用功能：把整个文件夹打包成 zip 文件下载。

异步编程简史

异步编程，能让程序具有同时处理多项任务的能力。例如，对于一个文件服务器来说，可能会有多个用户同时访问这个服务器，而服务器需要同时服务所有用户，让它们的体验尽可能流畅、低延时。在典型的异步程序，例如服务器中，每项任务的大部分时间都花在等待 IO 上，实际的计算时间占比较低。因此，我们并不需要很多的计算资源，也能同时处理大量任务。而这其中的诀窍，就是频繁地在多个任务之间切换：如果某项任务开始等待 IO，那么就不要继续处理它，而是马上切换到不需要等待的任务上。

过去，异步程序往往是通过多线程的方式实现的：每项任务对应一个操作系统的线程。然而，操作系统线程需要占用较多资源，而且在线程之间切换开销较大。因此，进入 21 世纪后，实现异步程序的主要方式变成了事件循环。整个异步程序的形态是一个巨大的循环，每次循环中，程序检查哪些 IO 操作已经完成，然后运行那些等待着这些已完成的 IO 操作的任务，直到它们发起下一次 IO 请求，重新进入等待状态。在这种编程范式中，任务间的切换发生在同一个用户态的线程里，因此开销极低。

然而，手写事件循环是一件非常痛苦的事情。因为同一个任务的代码会被拆散到多次不同的循环中执行，程序的逻辑变得不连贯了。因此，基于事件循环的程序非常难编写和调试。幸运的是，就像大部分其他现代编程语言一样，MoonBit 提供了原生的异步编程支持。用户可以像写同步程序一样写异步代码，MoonBit 会自动把异步代码切分成不同的部分。而 moonbitlang/async 库则提供了事件循环和各种 IO 原语的实现，负责把异步代码运行起来。

MoonBit 中的异步编程

在 MoonBit 中，可以用 async fn 语法来声明一个异步函数。异步函数看上去和同步函数完全一样，只不过它们在运行时可能在中途被打断，一段时间后才继续恢复运行，从而实现多个任务间的切换。在异步函数中可以正常使用循环等控制流构造，MoonBit 编译器会自动将它们变成异步的样子。

和许多其他语言不同，在调用异步函数时，MoonBit 不需要用 await 之类的特殊语法标记，编译器会自动推断出哪些函数调用是异步的。不过，如果你使用带有 MoonBit 支持的 IDE 或文本编辑器查看代码，就会看到异步函数调用被渲染成了斜体、可能抛出错误的函数调用带有下划线。因此，阅读代码时，依然可以一眼就找到所有异步的函数调用。

对于异步程序来说，另一个必不可少的组件是事件循环、任务调度和各种 IO 原语的实现。这一点在 MoonBit 中是通过 moonbitlang/async 库实现的。 moonbitlang/async 库中提供了网络IO、文件IO、进程创建等异步操作的支持，以及一系列管理异步编程任务的 API。接下来，我们将会在编写 HTTP 文件服务器的途中介绍 moonbitlang/async 的各种功能。

HTTP 服务器的骨架

典型的 HTTP 服务器的结构是：

服务器监听一个 TCP 端口，等待来自用户的连接请求
接受来自用户的 TCP 连接后，服务器从 TCP 连接中读取用户的请求，处理用户的请求并将结果发回给用户

这里的每一项任务，都应该异步地进行：在处理第一个用户的请求时，服务器仍应不断等待新的连接，并第一时间响应下一个用户的连接请求。如果有多个用户同时连接到服务器，服务器应该同时处理所有用户的请求。在这个过程中，所有可能耗费较多时间的操作，例如网络 IO 和文件 IO，都应该是异步的，它们不应该阻塞程序、影响其他任务的处理。

在 moonbitlang/async 中，有一个辅助函数 @http.run_server，能够绑我们自动完成上述工作，搭建一个 HTTP 服务器并运行它：

async fn async fn server_main(path~ : String, port~ : Int) -> Unit
server_main(String
path~ : String
String, Int
port~ : Int
Int) -> Unit
Unit {
  (Unit, (?, Unit) -> Unit) -> Unit
@http.run_server((String) -> Unit
@socket.Addr::(String) -> Unit
parse("[::]:\{Int
port}"), fn (?
conn, Unit
addr) {
    Unit
@pipe.stderr.(String) -> Unit
write("received new connection from \{Unit
addr}\n")
    async fn handle_connection(base_path : String, conn : ?) -> Unit
handle_connection(String
path, ?
conn)
  })
}

server_main 接受两个参数，其中， path 是文件服务器工作的路径，port 是服务器监听的端口。在 moonbitlang/async 中，一切异步代码都是可以取消的，而异步代码被取消时会抛出错误，所以所有异步函数都会抛出错误。因此，在 MoonBit 中，async fn 默认就会抛出错误，无需再显式标注 raise。

在 server_main 中，我们使用 @http.run_server 创建了一个 HTTP 服务器并运行它。 @http 是 moonbitlang/async 中提供 HTTP 解析等支持的包 moonbitlang/async/http 的别名， @http.run_server 的第一个参数是服务器要监听的地址。这里我们提供的地址是 [::]:port，这表示监听端口 port、接受来自任何网络接口的连接请求。 moonbitlang/async 有原生的 IPv4/IPv6 双栈支持，因此这里的服务器可以同时接受 IPv4 连接和 IPv6 连接。 @http.run_server 的第二个参数是一个回调函数，用于处理来自用户的连接。回调函数会接受两个参数，第一个是来自用户的连接，类型是 @http.ServerConnection，由 @http.run_server 自动获取并创建。第二个参数是用户的网络地址。这里，我们使用 handle_connection 函数来处理用户的请求，这个函数的实现将在稍后给出。 @http.run_server 会自动创建一个并行的任务，并在其中运行 handle_connection。因此，服务器可以同时运行多份 handle_connection、处理多个连接。

处理用户来自用户的请求

接下来，我们开始实现实际处理用户请求的 handle_connection 函数。 handle_connection 接受两个参数，base_path 是文件服务器处理的路径，而 conn 是来自用户的连接。

async fn async fn handle_connection(base_path : String, conn : ?) -> Unit
handle_connection(
  String
base_path : String
String,
  ?
conn : @http.ServerConnection,
) -> Unit
Unit {
  for {
    let Unit
request = ?
conn.() -> Unit
read_request()
    ?
conn.() -> Unit
skip_request_body()
    guard Unit
request.Unit
meth is Unit
Get else {
      ?
conn
      ..(Int, String) -> Unit
send_response(501, "Not Implemented")
      ..(String) -> Unit
write("This request is not implemented")
      ..() -> Unit
end_response()
    }
    let (String
path, Bool
download_zip) = match Unit
request.String
path {
      String
[ ..path, .."?download_zip" ] => (StringView
path.fn Show::to_string(self : StringView) -> String
Returns a new String containing a copy of the characters in this view.
Examples
  let str = "Hello World"
  let view = str.view(start_offset = str.offset_of_nth_char(0).unwrap(),end_offset = str.offset_of_nth_char(5).unwrap()) // "Hello"
  inspect(view.to_string(), content="Hello")
to_string(), true)
      String
path => (String
path, false)
    }
    if Bool
download_zip {
      async fn serve_zip(conn : ?, path : String) -> Unit
serve_zip(?
conn, String
base_path fn Add::add(self : String, other : String) -> String
Concatenates two strings, creating a new string that contains all characters
from the first string followed by all characters from the second string.
Parameters:

self : The first string to concatenate.
other : The second string to concatenate.
Returns a new string containing the concatenation of both input strings.
Example:
let hello = "Hello"
let world = " World!"
inspect(hello + world, content="Hello World!")
inspect("" + "abc", content="abc") // concatenating with empty string
+ String
path)
    } else {
      let ?
file = (String, Unit) -> ?
@fs.open(String
base_path fn Add::add(self : String, other : String) -> String
Concatenates two strings, creating a new string that contains all characters
from the first string followed by all characters from the second string.
Parameters:

self : The first string to concatenate.
other : The second string to concatenate.
Returns a new string containing the concatenation of both input strings.
Example:
let hello = "Hello"
let world = " World!"
inspect(hello + world, content="Hello World!")
inspect("" + "abc", content="abc") // concatenating with empty string
+ String
path, Unit
mode=Unit
ReadOnly) catch {
        _ => {
          ?
conn
          ..(Int, String) -> Unit
send_response(404, "NotFound")
          ..(String) -> Unit
write("File not found")
          ..() -> Unit
end_response()
          continue
        }
      }
      defer ?
file.() -> Unit
close()
      if ?
file.() -> Unit
kind() is Unit
Directory {
        if Bool
download_zip {
        } else {
          async fn serve_directory(conn : ?, dir : ?, path~ : String) -> Unit
serve_directory(?
conn, ?
file.() -> ?
as_dir(), String
path~)
        }
      } else {
        async fn server_file(conn : ?, file : ?, path~ : String) -> Unit
server_file(?
conn, ?
file, String
path~)
      }
    }
  }
}

在 handle_connection 中，程序通过一个大循环来不断从连接中读取用户请求并处理。每次循环中，我们首先通过 conn.read_request() 读取一个来自用户的请求。 conn.read_request() 只会读取 HTTP 请求的头部，这是为了允许用户流式地读取较大的 body。由于我们的文件服务器只处理 Get 请求，我们不需要请求的 body 中包含任何信息。因此，我们通过 conn.skip_body() 跳过用户请求的 body，以保证下一个请求的内容可以被正确读取。

接下来，如果遇到不是 Get 的请求，guard 语句的 else 块会被执行，此时，guard 语句后面的代码会被跳过，我们可以进入下一次循环、处理下一个请求。在 else 块中，通过 conn.send_response(..) 向用户发送一个 “不支持该请求” 的回复。 conn.send_response(..) 会发送回复的头部，这之后，我们用 conn.write(..) 向连接写入回复的主体内容。在写完所有内容后，我们需要用 conn.end_response() 来表明已经写完了回复的所有内容。

这里，我们希望实现一个 python -m http.server 中没有的实用功能：以 zip 的形式下载整个文件夹。如果用户请求的 URL 的形式是 /path/to/directory?download_zip，我们就把 /path/to/directory 打包成 .zip 文件发送给用户。这一功能是通过 serve_zip 函数来实现的。

由于我们实现的是一个文件服务器，用户的 GET 请求中指定的路径会直接映射到 base_path 下对应的路径。 @fs 是 moonbitlang/async 中提供文件 IO 支持的包 moonbitlang/async/fs 的别名。这里我们使用 @fs.open 打开对应的文件。如果打开文件失败了，我们向用户发送一个 404 回复，告诉用户这个文件不存在。

如果用户请求的文件是存在的，那么我们需要把文件发送给用户。当然，在此之前，别忘了用 defer file.close() 保证 file 占用的资源被及时释放。通过 file.kind()，我们可以获得文件的种类。在文件服务器中，如果用户请求的路径是一个文件夹，我们需要进行特殊的处理。因为文件夹不能直接被发送给用户，我们需要根据文件夹的内容，向用户返回一个 HTML 页面，让用户可以从页面看到文件夹里有哪些文件，并通过点击跳转到对应的页面。这部分功能通过函数 serve_directory 提供。如果用户请求的是一个普通文件，那么直接将文件的内容传输给用户即可。这部分功能通过函数 serve_file 来实现。

向用户发送一个普通文件的代码如下：

async fn async fn server_file(conn : ?, file : ?, path~ : String) -> Unit
server_file(
  ?
conn : @http.ServerConnection,
  ?
file : @fs.File,
  String
path~ : String
String,
) -> Unit
Unit {
  let String
content_type = match String
path {
    [.., .. ".png"] => "image/png"
    [.., .. ".jpg"] | "jpeg" => "image/jpeg"
    [.., .. ".html"] => "text/html"
    [.., .. ".css"] => "text/css"
    [.., .. ".js"] => "text/javascript"
    [.., .. ".mp4"] => "video/mp4"
    [.., .. ".mpv"] => "video/mpv"
    [.., .. ".mpeg"] => "video/mpeg"
    [.., .. ".mkv"] => "video/x-matroska"
    _ => "appliaction/octet-stream"
  }
  ?
conn
  ..(Int, String, Map[String, String]) -> Unit
send_response(200, "OK", Map[String, String]
extra_headers={ "Content-Type": String
content_type })
  ..(?) -> Unit
write_reader(?
file)
  ..() -> Unit
end_response()
}

这里，在 HTTP 回复中，我们根据文件的后缀名填入了不同的 Content-Type 字段。这样一来，用户在浏览器中打开图片/视频/HTML 文件时，就可以直接预览文件的内容，而不需要先下载文件再在本地打开。对于其他文件，Content-Type 字段的值会是 application/octet-stream，这会让浏览器自动将文件下载到本地。

我们依然使用 conn.send_response 来用户发送回复。通过 extra_headers 字段我们可以在回复中加入额外的 HTTP header。回复的主体则是文件的内容。这里，conn.write_reader 会自动流式地把 file 的内容发送给用户。假设用户请求了一个视频文件并在浏览器中播放，如果我们先把整个视频文件读到内存中再发送给用户，那么用户需要等服务器读入整个视频文件之后才能收到回复，服务器的响应速度会变慢。而且，读入整个视频文件会浪费大量的内存。而通过使用 write_reader，@http.ServerConnection 会自动把文件内容切成小块分段发送，用户马上就能看到视频开始播放，占用的内存也会大大减少。

接下来，让我们实现显示文件夹的函数 serve_directory：

async fn async fn serve_directory(conn : ?, dir : ?, path~ : String) -> Unit
serve_directory(
  ?
conn : @http.ServerConnection,
  ?
dir : @fs.Directory,
  String
path~ : String
String,
) -> Unit
Unit {
  let Unit
files = ?
dir.() -> Unit
read_all()
  Unit
files.() -> Unit
sort()
  ?
conn
  ..(Int, String, Map[String, String]) -> Unit
send_response(200, "OK", Map[String, String]
extra_headers={ "Content-Type": "text/html" })
  ..(String) -> Unit
write("<!DOCTYPE html><html><head></head><body>")
  ..(String) -> Unit
write("<h1>\{String
path}</h1>\n")
  ..(String) -> Unit
write("<div style=\"margin: 1em; font-size: 15pt\">\n")
  ..(String) -> Unit
write("<a href=\"\{String
path}?download_zip\">download as zip</a><br/><br/>\n")
  if String
path[:-1].fn StringView::rev_find(self : StringView, str : StringView) -> Int?
Returns the offset of the last occurrence of the given substring. If the
substring is not found, it returns None.
rev_find("/") is (Int) -> Int?
Some(Int
index) {
    let String
parent = if Int
index fn Eq::equal(self : Int, other : Int) -> Bool
Compares two integers for equality.
Parameters:

self : The first integer to compare.
other : The second integer to compare.
Returns true if both integers have the same value, false otherwise.
Example:
inspect(42 == 42, content="true")
inspect(42 == -42, content="false")
== 0 { "/" } else { String
path[:Int
index].fn Show::to_string(self : StringView) -> String
Returns a new String containing a copy of the characters in this view.
Examples
  let str = "Hello World"
  let view = str.view(start_offset = str.offset_of_nth_char(0).unwrap(),end_offset = str.offset_of_nth_char(5).unwrap()) // "Hello"
  inspect(view.to_string(), content="Hello")
to_string() }
    ?
conn.(String) -> Unit
write("<a href=\"\{String
parent}\">..</a><br/><br/>\n")
  }
  for Unit
file in Unit
files {
    let String
file_url = if String
pathfn String::op_get(self : String, idx : Int) -> Int
Returns the UTF-16 code unit at the given index.
Parameters:

string : The string to access.
index : The position in the string from which to retrieve the code unit.
This method has O(1) complexity.
[path.fn String::length(self : String) -> Int
Returns the number of UTF-16 code units in the string. Note that this is not
necessarily equal to the number of Unicode characters (code points) in the
string, as some characters may be represented by multiple UTF-16 code units.
Parameters:

string : The string whose length is to be determined.
Returns the number of UTF-16 code units in the string.
Example:
inspect("hello".length(), content="5")
inspect("🤣".length(), content="2") // Emoji uses two UTF-16 code units
inspect("".length(), content="0") // Empty string
length() fn Sub::sub(self : Int, other : Int) -> Int
Performs subtraction between two 32-bit integers, following standard two's
complement arithmetic rules. When the result overflows or underflows, it
wraps around within the 32-bit integer range.
Parameters:

self : The minuend (the number being subtracted from).
other : The subtrahend (the number to subtract).
Returns the difference between self and other.
Example:
let a = 42
let b = 10
inspect(a - b, content="32")
let max = 2147483647 // Int maximum value
inspect(max - -1, content="-2147483648") // Overflow case
- 1] (Int, Int) -> Bool
!= '/' {
      "\{String
path}/\{Unit
file}"
    } else {
      "\{String
path}\{Unit
file}"
    }
    ?
conn.(String) -> Unit
write("<a href=\"\{String
file_url}\">\{Unit
file}</a><br/>\n")
  }
  ?
conn
  ..(String) -> Unit
write("</div></body></html>")
  ..() -> Unit
end_response()
}

这里，我们首先读入文件夹中的文件列表并对它们进行排序。接下来，我们根据文件夹的内容，拼出一段 HTML 页面。 HTML 页面的主体内容是文件夹中的文件，每个文件对应一个链接，上面显示着文件名，点击链接就能跳转到对应的文件。这里，我们通过 HTML 的 <a> 元素来实现这一点。如果文件夹不是根目录，那么我们在页面开头放上一个特殊的链接 ..，点击它会跳转到上一级目录。此外，页面里还有一个 download as zip 的链接，点击这个链接就能把当前文件夹打包成 zip 后下载。

实现将文件夹打包成 zip 的功能

接下来，我们实现将文件夹打包成 zip 提供给用户的功能。这里，简单起见，我们使用系统的 zip 命令。 serve_zip 函数的实现如下：

async fn async fn serve_zip(conn : ?, path : String) -> Unit
serve_zip(
  ?
conn : @http.ServerConnection,
  String
path : String
String,
) -> Unit
Unit {
  let Unit
full_path = (String) -> Unit
@fs.realpath(String
path)
  let String
zip_name = if Unit
full_path[:].(String) -> Unit
rev_find("/") is (Int) -> Unit
Some(Int
i) {
    Unit
full_path[Int
i+1:].() -> String
to_string()
  } else {
    String
path
  }
  ((Unit) -> Unit) -> Unit
@async.with_task_group(fn(Unit
group) {
    let (Unit
we_read_from_zip, Unit
zip_write_to_us) = () -> (Unit, Unit)
@process.read_from_process()
    defer Unit
we_read_from_zip.() -> Unit
close()
    Unit
group.(() -> Unit) -> Unit
spawn_bg(fn() {
      let Int
exit_code = (String, Array[String], Unit) -> Int
@process.run(
        "zip",
        [ "-q", "-r", "-", String
path ],
        Unit
stdout=Unit
zip_write_to_us,
      )
      if Int
exit_code fn[T : Eq] @moonbitlang/core/builtin.op_notequal(x : T, y : T) -> Bool
!= 0 {
        fn[T] fail(msg : String, loc~ : SourceLoc = _) -> T raise Failure
Raises a Failure error with a given message and source location.
Parameters:

message : A string containing the error message to be included in the
failure.
location : The source code location where the failure occurred.
Automatically provided by the compiler when not specified.
Returns a value of type T wrapped in a Failure error type.
Throws an error of type Failure with a message that includes both the
source location and the provided error message.
fail("zip failed with exit code \{Int
exit_code}")
      }
    })
    ?
conn
    ..(Int, String, Map[String, String]) -> Unit
send_response(200, "OK", Map[String, String]
extra_headers={
      "Content-Type": "application/octet-stream",
      "Content-Disposition": "filename=\{String
zip_name}.zip",
    })
    ..(Unit) -> Unit
write_reader(Unit
we_read_from_zip)
    ..() -> Unit
end_response()
  })
}

在 serve_zip 函数的开头，我们首先计算了用户下载的 .zip 文件的文件名。接下来，我们使用 @async.with_task_group 创建了一个新的任务组。任务组是 moonbitlang/async 中用于管理异步任务的核心构造，所有异步任务都必须在一个任务组中创建。在介绍 with_task_group 之前，让我们先看看 serve_zip 剩下的内容。首先，我们使用 @process.read_from_process() 创建了一个临时管道，从管道的一端写入的数据可以从另一侧读出，因此它可以用于读取一个进程的输出。这里我们把管道的写入端 zip_write_to_us 会被提供给 zip 命令，用于写入压缩的结果。而我们将从管道的读入端 we_read_from_zip 读取 zip 命令的输出，并将其发送给用户。

接下来，我们在新的任务组中创建了一个单独的任务，并在其中使用 @process.run 运行 zip 命令。 @process 是 moonbitlang/async/process 的别名，是 moonbitlang/async 中提供调用外部进程功能的包。我们向 zip 传递的参数的意义是：

-q：不要输出日志信息
-r：递归压缩整个文件夹
-：把结果写入到 stdout
path：要压缩的文件夹

在调用 @process.run 时，我们通过 stdout=zip_write_to_us，把 zip 命令的 stdout 重定向到了 zip_write_to_us，以获取 zip 的输出。相比创建一个临时文件，这么做有两个好处：

和 zip 间的数据传递完全在内存中进行，不需要进行低效的磁盘 IO
zip 一边压缩，我们可以一边像用户发送已经压缩好的部分，效率更高

@process.run 会等待 zip 结束运行，并返回 zip 命令的状态码。如果 zip 的返回值不是 0，说明 zip 失败了，我们抛出一个错误。

在调用 zip 的同时，我们继续使用 conn.send_response(..) 向用户发送回复信息。接下来，我们用 conn.write_reader(we_read_from_zip) 把 zip 的输出发送给用户。 Content-Disposition 这一 HTTP header 能让我们指定用户下载的 zip 文件的名字。

到这里，一切看上去都很合理。但为什么这里要创建一个新的任务组呢？为什么不能直接提供创建新任务的 API 呢？在编写异步程序时，有一个现象：写出在正确时行为正确的程序比较容易，但写出在出错时依然行为正确的程序很难。比如，对于 serve_zip 这个例子：

如果 zip 命令失败了我们应该怎么办？
如果数据发送到一半发生了网络错误，或者用户关闭了连接，应该怎么办？

如果 zip 命令失败了，那么整个 serve_zip 函数也应该失败。由于此时用户可能已经收到了一部分不完整的数据，我们很难再把连接恢复到正常状态，只能关闭把整个连接。如果数据发送到一半发生了网络错误，那么我们应该停止 zip 的运行。因为此时 zip 的结果已经没有用了，让它继续运行只是在浪费资源。而且在最坏的情况下，由于我们不再读取 zip 的输出，和 zip 通信用的管道可能会被填满，此时，zip 可能会永远阻塞在向管道写入的操作上，变成一个僵尸进程。

在上面的代码中，我们没有显式地写任何错误处理逻辑，但是，在出现上述错误时，我们的程序的行为却是符合预期的，而魔法就在于 @async.with_task_group 的语义，及其背后的 结构化并发 范式。 @async.with_task_group(f) 的大致语义如下：

它会创建一个新的任务组 group，并运行 f(group)
f 可以通过 group.spawn_bg(..) 等函数在 group 中创建新的任务
只有当 group 中的所有任务都完成时，with_task_group 才会返回
如果 group 中的任何一个任务失败了，那么 with_task_group 也会失败，group 中的其他任务会被自动取消

这里的最后一条，就是保证正确错误处理的行为的关键：

如果调用 zip 的任务失败了，那么错误会传播到整个任务组。向用户发送回复的主任务会自动被取消，然后错误会通过 with_task_group 自动向上传播，关闭连接
如果发送回复的主任务失败了，错误同样会传播到整个任务组。此时 @process.run 会被取消，此时它会自动向 zip 发送终止信号，结束 zip 的运行

因此，在使用 moonbitlang/async 编写异步程序时，只需要根据程序的结构在适当的位置插入任务组，剩下的错误处理的所有细节，都会由 with_task_group 自动解决。这正是 moonbitlang/async 使用的结构化并发范式的威力：通过编程范式的引导，它能让我们写出结构更清晰的异步程序，并以一种润物细无声的方式，让异步程序在出错时也能有正确的行为。

让服务器跑起来

至此，整个 HTTP 服务器的所有内容都已实现完毕，我们可以运行这个服务器了。 MoonBit 对异步代码有原生支持，可以直接用 async fn main 定义异步程序的入口，或是用 async test 直接测试异步代码。这里，我们让 HTTP 服务器运行在当前目录、向用户提供当前目录下的文件，并让它监听 8000 端口：

async test {
  async fn server_main(path~ : String, port~ : Int) -> Unit
server_main(String
path=".", Int
port=8000)
}

通过 moon test moonbit_http_server.mbt.md 运行这份文档的源码，并在浏览器中打开 http://127.0.0.1:8000，即可使用我们实现的文件服务器。

关于 moonbitlang/async 的更多功能，可以参考它的 API 文档和 GitHub repo。

初探 MoonBit 中的 JavaScript 交互

2025年9月25日 · 阅读需 14 分钟

引言

在当今的软件世界中，任何一门编程语言都无法成为一座孤岛。对于 MoonBit 这样一门新兴的通用编程语言而言，若想在庞大的技术生态中茁壮成长，与现有生态系统的无缝集成便显得至关重要。

MoonBit 提供了包括 JavaScript 在内的多种编译后端，这为其对接广阔的 JavaScript 生态敞开了大门。无论是对于浏览器前端开发，还是对于 Node.js 环境下的后端应用，这种集成能力都极大地拓展了 MoonBit 的应用场景，让开发者可以在享受 MoonBit 带来的类型安全与高性能的同时，复用数以万计的现有 JavaScript 库。

在本文中，我们将以 Node.js 环境为例，一步步探索 MoonBit JavaScript FFI 的奥秘，从基础的函数调用到复杂的类型与错误处理，向你展示如何优雅地搭建连接 MoonBit 与 JavaScript 世界的桥梁。

预先准备

在正式启程之前，我们需要先为项目做好基础配置。如果还没有现成的项目，可以使用 moon new 工具创建一个新的 MoonBit 项目。

为了让 MoonBit 工具链知晓我们的目标平台是 JavaScript，我们需要在项目根目录的 moon.mod.json 文件中添加以下内容：

{
  "preferred-target": "js"
}

此项配置会告知编译器，在执行 moon build 或 moon check 等命令时，默认使用 JavaScript 后端。当然，如果你希望在命令行中临时指定，也可以通过 --target=js 参数达到同样的效果。

编译项目

完成上述配置后，只需在项目根目录下运行我们所熟悉的构建命令：

> moon build

命令执行成功后，由于我们的项目默认包含一个可执行入口，你可以在 target/js/debug/build/ 目录下找到编译产物。MoonBit 非常贴心地为我们生成了三个文件：

.js 文件：编译后的 JavaScript 源码。
.js.map 文件：用于调试的 Source Map 文件。
.d.ts 文件：TypeScript 类型声明文件，便于在 TypeScript 项目中集成。

第一个 JavaScript API 调用

MoonBit 的 FFI 设计在原则上保持了一致性。与调用 C 或其他语言类似，我们通过一个带有 extern 关键字的函数声明来定义一个外部调用：

extern "js" fn consoleLog(msg : String
String) -> Unit
Unit = "(msg) => console.log(msg)"

这行代码是 FFI 的核心。让我们来分解一下：

extern "js"：声明这是一个指向 JavaScript 环境的外部函数。
fn consoleLog(msg : String) -> Unit：这是该函数在 MoonBit 中的类型签名，它接受一个 String 类型的参数，并且返回一个单位值 (Unit)。
"(msg) => console.log(msg)"：等号右侧的字符串字面量是这段 FFI 的“灵魂”，其中需要包含一段原生 JavaScript 函数。

在这里，我们使用了一个简洁的箭头函数。 MoonBit 编译器会按原样将这段代码嵌入到最终生成的 .js 文件中，从而实现从 MoonBit 到 JavaScript 的调用。

提示如果你的 JavaScript 代码片段比较复杂，可以使用 #| 语法来定义多行字符串，以提高可读性。

一旦这个 FFI 声明就绪，我们就可以在 MoonBit 代码中像调用普通函数一样调用 consoleLog 了：

test "hello" {
  fn consoleLog(msg : String) -> Unit
consoleLog("Hello from JavaScript!")
}

运行 moon test，你将会在控制台看到由 JavaScript console.log 打印出的信息。我们的第一座桥梁已经成功搭建！

JavaScript 类型的对接

打通调用流程只是第一步，真正的挑战在于如何处理两种语言之间的类型差异。 MoonBit 是一门静态类型语言，而 JavaScript 则是动态类型语言。如何在这两者之间建立安全可靠的类型映射，是 FFI 设计中需要重点考虑的问题。

下面，我们从易到难，分情况介绍如何在 MoonBit 中对接不同的 JavaScript 类型。

无需转换的 JavaScript 类型

最简单的情况是，MoonBit 中的某些类型在编译到 JavaScript 后端时，其底层实现本身就是对应的原生 JavaScript 类型。在这种情况下，我们可以直接进行传递，无需任何转换。

常见的“零成本”对接类型如下表所示：

MoonBit 类型	JavaScript 对应类型
`String`	`string`
`Bool`	`boolean`
`Int`, `UInt`, `Float`, `Double`	`number`
`BigInt`	`bigint`
`Bytes`	`Uint8Array`
`Array[T]`	`Array<T>`
函数类型	`Function`

基于这些对应关系，我们已经能够对许多简单的 JavaScript 函数进行绑定了。事实上，在之前绑定 console.log 函数的例子中，我们已经使用了 MoonBit 中 String 类型与 JavaScript 中 string 类型的对应关系。

注意：维持 MoonBit 类型的内部不变量

一个非常重要的细节是，MoonBit 的所有标准数值类型（Int, Float 等）在 JavaScript 中都对应于 number 类型，即 IEEE 754 双精度浮点数。这意味着当整数值越过 FFI 边界进入 JavaScript 后，其行为将遵循浮点数语义，这可能会导致在 MoonBit 看来非预期的结果，例如整数溢出行为的差异：

extern "js" fn incr(x : Int
Int) -> Int
Int = "(x) => x + 1"

test "incr" {
  // 在 MoonBit 中，@int.max_value + 1 会溢出并回绕
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(let @moonbitlang/core/int.max_value : Int
Maximum value of an integer.
@int.max_value fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ 1, String
content="-2147483648")
  // 在 JavaScript 中，它被当作浮点数处理，不会溢出
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn incr(x : Int) -> Int
incr(let @moonbitlang/core/int.max_value : Int
Maximum value of an integer.
@int.max_value), String
content="2147483648") // ???
}

而这本质上是不合法的，因为根据 MoonBit 中 Int 的值的内部不变量，其值不可能是 2147483648（超出了类型允许的最大值）。这可能导致下游依赖这一点的其他 MoonBit 代码出现意料之外的行为。在跨越 FFI 边界处理其他数据类型时也有可能出现类似的问题，因此请在编写相关逻辑时务必留意这一点。

外部 JavaScript 类型

当然，JavaScript 的世界远比上述基本类型要丰富。我们很快就会遇到 undefined、null、symbol 以及各种复杂的宿主对象（Host Object）。这些类型在 MoonBit 中没有直接的对应物。

对于这种情况，MoonBit 提供了 #external 注解。这个注解好比一个契约，它告诉编译器： “请相信我，这个类型在外部世界（JavaScript）中是真实存在的。你不需要关心它的内部结构，只需把它当作一个不透明的句柄来处理即可。”

例如，我们可以这样定义一个代表 JavaScript undefined 的类型：

#external
type Undefined

extern "js" fn Undefined::new() -> Self = "() => undefined"

然而，单独的 Undefined 类型意义不大，因为在实际应用中，undefined 往往是作为联合类型（Union Type）的一部分出现的，例如 string | undefined。

一个更实用的方案是创建一个 Optional[T] 类型来精确对应 JavaScript 中的 T | undefined，并让它能与 MoonBit 内置的 T?（Option[T]）类型方便地互相转换。

为了实现这个目标，我们首先需要一个能够代表“任意” JavaScript 值的类型，类似于 TypeScript 中的 any。这正是 #external 的用武之地：

#external
pub type Value

相应地，我们还需要提供获取 undefined 值和判断某值是否为 undefined 的方法：

extern "js" fn type Value
Value::undefined() -> type Value
Value =
  #| () => undefined

extern "js" fn type Value
Value::is_undefined(self : type Value
Self) -> Bool
Bool =
  #| (n) => Object.is(n, undefined)

为了方便调试，我们再为 Value 类型实现 Show 特质，让它可以被打印出来：

pub impl trait Show {
  output(Self, &Logger) -> Unit
  to_string(Self) -> String
}
Trait for types that can be converted to String
Show for type Value
Value with fn Show::output(self : Value, logger : &Logger) -> Unit
output(Value
self, &Logger
logger) {
  &Logger
logger.fn Logger::write_string(&Logger, String) -> Unit
write_string(Value
self.fn Value::to_string(self : Value) -> String
to_string())
}

pub extern "js" fn type Value
Value::to_string(self : type Value
Value) -> String
String =
  #| (self) =>
  #|   self === undefined ? 'undefined'
  #|     : self === null ? 'null'
  #|     : self.toString()

接下来是整个转换过程中的“魔法”所在。我们定义两个特殊的转换函数：

fn[T] type Value
Value::cast_from(value : type parameter T
T) -> type Value
Value = "%identity"

fn[T] type Value
Value::cast(self : type Value
Self) -> type parameter T
T = "%identity"

何为 %identity

%identity 是 MoonBit 提供的一个特殊内建函数（intrinsic），它是一个“零成本”的类型转换操作。它在编译时会进行类型检查，但在运行时不会产生任何效果。它仅仅是告诉编译器：“作为开发者，我比你更清楚这个值的真实类型，请直接将它当作另一种类型来看待。”

这是一把双刃剑：它为 FFI 边界层的代码提供了强大的表达能力，但如果滥用，则可能破坏类型安全。因此，它的使用场景应当被严格限制在 FFI 相关代码范围内。

有了这些积木，我们就可以开始搭建 Optional[T] 了：

#external
type Optional[_] // 对应 T | undefined

/// 创建一个 undefined 的 Optional
fn[T] type Optional[_]
Optional::fn[T] Optional::undefined() -> Optional[T]
创建一个 undefined 的 Optional
undefined() -> type Optional[_]
Optional[type parameter T
T] {
  type Value
Value::fn Value::undefined() -> Value
undefined().fn[T] Value::cast(self : Value) -> T
cast()
}

/// 检查一个 Optional 是否为 undefined
fn[T] type Optional[_]
Optional::fn[T] Optional::is_undefined(self : Optional[T]) -> Bool
检查一个 Optional 是否为 undefined
is_undefined(Optional[T]
self : type Optional[_]
Optional[type parameter T
T]) -> Bool
Bool {
  Optional[T]
self |> type Value
Value::fn[T] Value::cast_from(value : T) -> Value
cast_from |> type Value
Value::fn Value::is_undefined(self : Value) -> Bool
is_undefined
}

/// 从 Optional[T] 中解包出 T，如果为 undefined 则 panic
fn[T] type Optional[_]
Optional::fn[T] Optional::unwrap(self : Optional[T]) -> T
从 Optional[T] 中解包出 T，如果为 undefined 则 panic
unwrap(Optional[T]
self : type Optional[_]
Self[type parameter T
T]) -> type parameter T
T {
  guard Bool
!Optional[T]
selfBool
.fn[T] Optional::is_undefined(self : Optional[T]) -> Bool
检查一个 Optional 是否为 undefined
is_undefinedBool
() else { fn[T] abort(string : String, loc~ : SourceLoc = _) -> T
abort("Cannot unwrap an undefined value") }
  type Value
Value::fn[T] Value::cast_from(value : T) -> Value
cast_from(Optional[T]
self).fn[T] Value::cast(self : Value) -> T
cast()
}

/// 将 Optional[T] 转换为 MoonBit 内置的 T?
fn[T] type Optional[_]
Optional::fn[T] Optional::to_option(self : Optional[T]) -> T?
将 Optional[T] 转换为 MoonBit 内置的 T?
to_option(Optional[T]
self : type Optional[_]
Optional[type parameter T
T]) -> type parameter T
T? {
  guard Bool
!type Value
ValueBool
::fn[T] Value::cast_from(value : T) -> Value
cast_fromBool
(Optional[T]
selfBool
).fn Value::is_undefined(self : Value) -> Bool
is_undefinedBool
() else { T?
None }
  (T) -> T?
Some(type Value
Value::fn[T] Value::cast_from(value : T) -> Value
cast_from(Optional[T]
self).fn[T] Value::cast(self : Value) -> T
cast())
}

/// 从 MoonBit 内置的 T? 创建 Optional[T]
fn[T] type Optional[_]
Optional::fn[T] Optional::from_option(value : T?) -> Optional[T]
从 MoonBit 内置的 T? 创建 Optional[T]
from_option(T?
value : type parameter T
T?) -> type Optional[_]
Optional[type parameter T
T] {
  guard T?
value is (T) -> T?
Some(T
v) else { type Optional[_]
Optional::fn[T] Optional::undefined() -> Optional[T]
创建一个 undefined 的 Optional
undefined() }
  type Value
Value::fn[T] Value::cast_from(value : T) -> Value
cast_from(T
v).fn[T] Value::cast(self : Value) -> T
cast()
}

test "Optional from and to Option" {
  let Optional[Int]
optional = type Optional[_]
Optional::fn[T] Optional::from_option(value : T?) -> Optional[T]
从 MoonBit 内置的 T? 创建 Optional[T]
from_option((Int) -> Int?
Some(3))
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Optional[Int]
optional.fn[T] Optional::unwrap(self : Optional[T]) -> T
从 Optional[T] 中解包出 T，如果为 undefined 则 panic
unwrap(), String
content="3")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Optional[Int]
optional.fn[T] Optional::is_undefined(self : Optional[T]) -> Bool
检查一个 Optional 是否为 undefined
is_undefined(), String
content="false")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Optional[Int]
optional.fn[T] Optional::to_option(self : Optional[T]) -> T?
将 Optional[T] 转换为 MoonBit 内置的 T?
to_option(), String
content="Some(3)")
  let Optional[Int]
optional : type Optional[_]
Optional[Int
Int] = type Optional[_]
Optional::fn[T] Optional::from_option(value : T?) -> Optional[T]
从 MoonBit 内置的 T? 创建 Optional[T]
from_option(Int?
None)
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Optional[Int]
optional.fn[T] Optional::is_undefined(self : Optional[T]) -> Bool
检查一个 Optional 是否为 undefined
is_undefined(), String
content="true")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Optional[Int]
optional.fn[T] Optional::to_option(self : Optional[T]) -> T?
将 Optional[T] 转换为 MoonBit 内置的 T?
to_option(), String
content="None")
}

通过这套组合拳，我们成功地在 MoonBit 的类型系统中为 T | undefined 找到了一个安全且人体工学良好的表达方式。同样的方法也可以用于对接 null、symbol、RegExp 等其他 JavaScript 特有的类型。

处理 JavaScript 错误

一个健壮的 FFI 层必须能够优雅地处理错误。默认情况下，如果在 FFI 调用中，JavaScript 代码抛出了一个异常，这个异常并不会被 MoonBit 的 try-catch 机制捕获，而是会直接中断整个程序的执行：

// 这是一个会抛出异常的 FFI 调用
extern "js" fn boom_naive() -> Value raise = "(u) => undefined.toString()"

test "boom_naive" {
  // 这段代码会直接让测试进程崩溃，而不是通过 `try?` 返回一个 `Result`
  inspect(try? boom_naive()) // failed: TypeError: Cannot read properties of undefined (reading 'toString')
}

正确的做法是在 JavaScript 层用 try...catch 语句将调用包裹起来，然后找到一种办法将成功的结果或捕获到的错误传递回 MoonBit。当然，我们可以直接在 extern "js" 声明的 JavaScript 代码中这么做，但也存在更可复用的解决办法：

首先，我们定义一个 Error_ 类型来封装来自 JavaScript 的错误：

suberror Error_ type Value
Value

pub impl trait Show {
  output(Self, &Logger) -> Unit
  to_string(Self) -> String
}
Trait for types that can be converted to String
Show for suberror Error_ Value
Error_ with fn Show::output(self : Error_, logger : &Logger) -> Unit
output(Error_
self, &Logger
logger) {
  &Logger
logger.fn Logger::write_string(&Logger, String) -> Unit
write_string("@js.Error: ")
  let (Value) -> Error_
Error_(Value
inner) = Error_
self
  &Logger
logger.fn[Obj : Show] Logger::write_object(self : &Logger, obj : Obj) -> Unit
write_object(Value
inner)
}

接着，我们定义一个核心的 FFI 包装函数 Error_::wrap_ffi。它的作用是在 JavaScript 领域执行一个操作（op），并根据成功与否，调用不同的回调函数（on_ok 或 on_error）：

extern "js" fn suberror Error_ Value
Error_::wrap_ffi(
  op : () -> type Value
Value,
  on_ok : (type Value
Value) -> Unit
Unit,
  on_error : (type Value
Value) -> Unit
Unit,
) -> Unit
Unit =
  #| (op, on_ok, on_error) => { try { on_ok(op()); } catch (e) { on_error(e); } }

最后，我们利用这个 FFI 函数和 MoonBit 的闭包，就可以封装出一个符合 MoonBit 风格、返回 T raise Error_ 的 Error_::wrap 函数：

fn[T] suberror Error_ Value
Error_::fn[T] Error_::wrap(op : () -> Value, map_ok? : (Value) -> T) -> T raise Error_
wrap(
  () -> Value
op : () -> type Value
Value,
  (Value) -> T
map_ok~ : (type Value
Value) -> type parameter T
T = type Value
Value::fn[T] Value::cast(self : Value) -> T
cast,
) -> type parameter T
T raise suberror Error_ Value
Error_ {
  // 定义一个变量，用于在闭包内外传递结果
  let mut Result[Value, Error_]
res : enum Result[A, B] {
  Err(B)
  Ok(A)
}
Result[type Value
Value, suberror Error_ Value
Error_] = (Value) -> Result[Value, Error_]
Ok(type Value
Value::fn Value::undefined() -> Value
undefined())
  // 调用 FFI，传入两个闭包，它们会根据 JS 的执行结果修改 res 的值
  suberror Error_ Value
Error_::fn Error_::wrap_ffi(op : () -> Value, on_ok : (Value) -> Unit, on_error : (Value) -> Unit) -> Unit
wrap_ffi(() -> Value
op, fn(Value
v) { Result[Value, Error_]
res = (Value) -> Result[Value, Error_]
Ok(Value
v) }, fn(Value
e) { Result[Value, Error_]
res = (Error_) -> Result[Value, Error_]
Err((Value) -> Error_
Error_(Value
e)) })
  // 检查 res 的值，并返回相应的结果或抛出错误
  match Result[Value, Error_]
res {
    (Value) -> Result[Value, Error_]
Ok(Value
v) => (Value) -> T
map_ok(Value
v)
    (Error_) -> Result[Value, Error_]
Err(Error_
e) => raise Error_
e
  }
}

现在，我们可以安全地调用之前那个会抛出异常的函数了，并且能以纯 MoonBit 代码来处理可能发生的错误：

extern "js" fn boom() -> type Value
Value = "(u) => undefined.toString()"

test "boom" {
  let Result[Value, Error_]
result = try? suberror Error_ Value
Error_::fn[T] Error_::wrap(op : () -> Value, map_ok? : (Value) -> T) -> T raise Error_
wrap(fn boom() -> Value
boom)
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    (Result[Value, Error_]
result : enum Result[A, B] {
  Err(B)
  Ok(A)
}
Result[type Value
Value, suberror Error_ Value
Error_]),
    String
content="Err(@js.Error: TypeError: Cannot read properties of undefined (reading 'toString'))",
  )
}

对接外部 JavaScript API

至此，我们已经掌握了处理类型和错误的关键技术，是时候将目光投向更广阔的天地了——整个 Node.js 和 NPM 生态系统。而这一切的入口，就是对 require() 函数的绑定。

extern "js" fn require_ffi(path : String
String) -> type Value
Value = "(path) => require(path)"

/// 一个更方便的包装，支持链式获取属性，例如 require("a", keys=["b", "c"])
pub fn fn require(path : String, keys? : Array[String]) -> Value
一个更方便的包装，支持链式获取属性，例如 require("a", keys=["b", "c"])
require(String
path : String
String, Array[String]
keys~ : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[String
String] = []) -> type Value
Value {
  Array[String]
keys.fn[A, B] Array::fold(self : Array[A], init~ : B, f : (B, A) -> B raise?) -> B raise?
Fold out values from an array according to certain rules.
Example:
let sum = [1, 2, 3, 4, 5].fold(init=0, (sum, elem) => sum + elem)
assert_eq(sum, 15)
fold(Value
init=fn require_ffi(path : String) -> Value
require_ffi(String
path), type Value
Value::fn[T] Value::get_with_string(self : Value, key : String) -> T
get_with_string)
}

// ... 其中 Value::get_with_string 的定义如下：

fn[T] type Value
Value::fn[T] Value::get_with_string(self : Value, key : String) -> T
get_with_string(Value
self : type Value
Self, String
key : String
String) -> type parameter T
T {
  Value
self.fn Value::get_ffi(self : Value, key : Value) -> Value
get_ffi(type Value
Value::fn[T] Value::cast_from(value : T) -> Value
cast_from(String
key)).fn[T] Value::cast(self : Value) -> T
cast()
}

extern "js" fn type Value
Value::get_ffi(self : type Value
Self, key : type Value
Self) -> type Value
Self = "(obj, key) => obj[key]"

有了这个 require 函数，我们就可以轻松加载 Node.js 的内置模块，例如 node:path 模块，并调用它的方法：

// 加载 node:path 模块的 basename 函数
let (String) -> String
basename : (String
String) -> String
String = fn require(path : String, keys~ : Array[String]) -> Value
一个更方便的包装，支持链式获取属性，例如 require("a", keys=["b", "c"])
require("node:path", Array[String]
keys=["basename"]).fn[T] Value::cast(self : Value) -> T
cast()

test "require Node API" {
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(let basename : (String) -> String
basename("/foo/bar/baz/asdf/quux.html"), String
content="quux.html")
}

更令人兴奋的是，使用同样的方法，我们还能调用 NPM 上的海量第三方库。让我们以一个流行的统计学计算库 simple-statistics 为例。

首先，我们需要像在一个标准的 JavaScript 项目中那样，初始化 package.json 并安装依赖。这里我们使用 pnpm，你也可以换成 npm 或 yarn：

> pnpm init
> pnpm install simple-statistics

准备工作就绪后，我们就可以在 MoonBit 代码中直接 require 这个库，并获取其中的 standardDeviation 函数：

let (Array[Double]) -> Double
standard_deviation : (type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[Double
Double]) -> Double
Double = fn require(path : String, keys~ : Array[String]) -> Value
一个更方便的包装，支持链式获取属性，例如 require("a", keys=["b", "c"])
require(
  "simple-statistics",
  Array[String]
keys=["standardDeviation"],
).fn[T] Value::cast(self : Value) -> T
cast()

现在，无论是 moon run 还是 moon test，MoonBit 都能正确地通过 Node.js 加载依赖并执行代码，返回我们期望的计算结果。

test "require external lib" {
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(let standard_deviation : (Array[Double]) -> Double
standard_deviation([2, 4, 4, 4, 5, 5, 7, 9]), String
content="2")
}

这无疑是激动人心的。仅仅通过几行 FFI 代码，我们就将 MoonBit 的类型安全世界与 NPM 庞大、成熟的生态系统连接在了一起。

结语

通过本文的探索，我们初步了解了如何在 MoonBit 语言中与 JavaScript 进行交互，从最基础的类型对接到复杂的错误处理，再到外部库的轻松集成。这些功能在 MoonBit 的静态类型系统与作为动态类型语言的 JavaScript 之间架起了一座桥梁，这体现了 MoonBit 作为现代编程语言在跨语言互操作性方面的思考。它让开发者既能享受到 MoonBit 的类型安全与现代化的语言特性，又能无缝访问 JavaScript 的庞大生态，为 MoonBit 拓宽了不可估量的应用前景。

当然，能力越大，责任也越大：FFI 虽然强大，但在实际开发中仍需谨慎处理类型转换和错误边界，确保程序的健壮性。

对于希望利用 JavaScript 库来扩展 MoonBit 应用功能的开发者来说，掌握这些 FFI 技术将是一项至关重要的技能。通过合理运用这些技术，我们可以构建出既具有 MoonBit 语言优势，又能充分利用 JavaScript 生态资源的高质量应用程序。

如果希望了解关于 MoonBit 在 JavaScript 互操作方面的探索进展的更多内容，欢迎关注基于 MoonBit 构建的 Web 应用前端 mooncakes.io 及其背后的界面库 rabbit-tea。

正则表达式引擎的两种实现方法：导数与 Thompson 虚拟机

2025年9月10日 · 阅读需 12 分钟

正则表达式引擎的实现方式多样，不同方法在性能、内存消耗和实现复杂度上各有权衡。本文将介绍两种数学上等价但实际表现迥异的正则匹配方法：Brzozowski 导数方法和 Thompson 虚拟机方法。

这两种方法都基于相同的抽象语法树表示，为直接的性能对比提供了统一的基础。其核心思想在于：这些看似不同的方法实际上是用不同的计算策略来解决同一个问题——一个依靠代数变换，另一个则通过程序执行。

约定与定义

为了建立统一的基础，两种正则表达式引擎都采用相同的抽象语法树（AST）表示，用树形结构来描述正则表达式的基本构造：

enum Ast {
  (Char) -> Ast
Chr(Char
Char)
  (Ast, Ast) -> Ast
Seq(enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast, enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast)
  (Ast, Int?) -> Ast
Rep(enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast, Int
Int?)
  (Ast) -> Ast
Opt(enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast)
} derive(trait Show {
  output(Self, &Logger) -> Unit
  to_string(Self) -> String
}
Trait for types that can be converted to String
Show, trait ToJson {
  to_json(Self) -> Json
}
Trait for types that can be converted to Json
ToJson, trait Hash {
  hash_combine(Self, Hasher) -> Unit
  hash(Self) -> Int
}
Trait for types that can be hashed
The hash method should return a hash value for the type, which is used in hash tables and other data structures.
The hash_combine method is used to combine the hash of the current value with another hash value,
typically used to hash composite types.
When two values are equal according to the Eq trait, they should produce the same hash value.
The hash method does not need to be implemented if hash_combine is implemented,
When implemented separately, hash does not need to produce a hash value that is consistent with hash_combine.
Hash, trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq)

此外，我们还提供了智能构造函数来简化正则表达式的构建：

fn enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast::fn Ast::chr(chr : Char) -> Ast
chr(Char
chr : Char
Char) -> enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast {
  (Char) -> Ast
Chr(Char
chr)
}

fn enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast::fn Ast::seq(self : Ast, other : Ast) -> Ast
seq(Ast
self : enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast, Ast
other : enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast) -> enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast {
  (Ast, Ast) -> Ast
Seq(Ast
self, Ast
other)
}

fn enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast::fn Ast::rep(self : Ast, n? : Int) -> Ast
rep(Ast
self : enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast, Int?
n? : Int
Int) -> enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast {
  (Ast, Int?) -> Ast
Rep(Ast
self, Int?
n)
}

fn enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast::fn Ast::opt(self : Ast) -> Ast
opt(Ast
self : enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast) -> enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast {
  Unit
@fs.
  (Ast) -> Ast
Opt(Ast
self)
}

AST 定义了四种基本的正则表达式操作：

Chr(Char) - 匹配单个字符字面量
Seq(Ast, Ast) - 序列匹配，即一个模式紧跟另一个模式
Rep(Ast, Int?) - 重复匹配，None 表示无限次重复，Some(n) 表示恰好重复 n 次
Opt(Ast) - 可选匹配，相当于标准正则语法中的 pattern?

举个例子，正则表达式 (ab*)? 表示一个可选的序列（'a' 后跟零个或多个 'b'），可以这样构建：

Ast::chr('a').seq(Ast::chr('b').rep()).opt()

Brzozowski 导数方法

导数方法基于形式语言理论，通过代数变换来处理正则表达式。对于输入的每个字符，该方法计算正则表达式的"导数"，实质上是在问："消费掉这个字符后，还剩下什么需要匹配？"这样就得到了一个新的正则表达式，代表剩余的匹配模式。

为了明确表示导数和可空性，我们对基本的 Ast 类型进行了扩展：

enum Exp {
  Exp
Nil
  Exp
Eps
  (Char) -> Exp
Chr(Char
Char)
  (Exp, Exp) -> Exp
Alt(enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp, enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp)
  (Exp, Exp) -> Exp
Seq(enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp, enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp)
  (Exp) -> Exp
Rep(enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp)
} derive(trait Show {
  output(Self, &Logger) -> Unit
  to_string(Self) -> String
}
Trait for types that can be converted to String
Show, trait Hash {
  hash_combine(Self, Hasher) -> Unit
  hash(Self) -> Int
}
Trait for types that can be hashed
The hash method should return a hash value for the type, which is used in hash tables and other data structures.
The hash_combine method is used to combine the hash of the current value with another hash value,
typically used to hash composite types.
When two values are equal according to the Eq trait, they should produce the same hash value.
The hash method does not need to be implemented if hash_combine is implemented,
When implemented separately, hash does not need to produce a hash value that is consistent with hash_combine.
Hash, trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq, trait Compare {
  compare(Self, Self) -> Int
  op_lt(Self, Self) -> Bool
  op_gt(Self, Self) -> Bool
  op_le(Self, Self) -> Bool
  op_ge(Self, Self) -> Bool
}
Trait for types whose elements are ordered
The return value of [compare] is:

zero, if the two arguments are equal
negative, if the first argument is smaller
positive, if the first argument is greater
Compare, trait ToJson {
  to_json(Self) -> Json
}
Trait for types that can be converted to Json
ToJson)

Exp 中各构造器的含义如下：

Nil - 表示不可能匹配的模式，即空集
Eps - 匹配空字符串
Chr(Char) - 匹配单个字符
Alt(Exp, Exp) - 表示选择（或），在多个模式间进行选择
Seq(Exp, Exp) - 表示连接，将两个模式依次连接
Rep(Exp) - 表示重复，对模式进行零次或多次重复

通过 Exp::of_ast 函数，我们可以将 Ast 转换为表达能力更强的 Exp 格式：

fn enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::of_ast(ast : Ast) -> Exp
of_ast(Ast
ast : enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast) -> enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp {
  match Ast
ast {
    (Char) -> Ast
Chr(Char
c) => (Char) -> Exp
Chr(Char
c)
    (Ast, Ast) -> Ast
Seq(Ast
a, Ast
b) => (Exp, Exp) -> Exp
Seq(enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::of_ast(ast : Ast) -> Exp
of_ast(Ast
a), enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::of_ast(ast : Ast) -> Exp
of_ast(Ast
b))
    (Ast, Int?) -> Ast
Rep(Ast
a, Int?
None) => (Exp) -> Exp
Rep(enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::of_ast(ast : Ast) -> Exp
of_ast(Ast
a))
    (Ast, Int?) -> Ast
Rep(Ast
a, (Int) -> Int?
Some(Int
n)) => {
      let Exp
sec = enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::of_ast(ast : Ast) -> Exp
of_ast(Ast
a)
      let mut Exp
exp = Exp
sec
      for _ in Int
1..<Int
n {
        Exp
exp = (Exp, Exp) -> Exp
Seq(Exp
exp, Exp
sec)
      }
      Exp
exp
    }
    (Ast) -> Ast
Opt(Ast
a) => (Exp, Exp) -> Exp
Alt(enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::of_ast(ast : Ast) -> Exp
of_ast(Ast
a), Exp
Eps)
  }
}

同样，我们也为 Exp 提供了智能构造函数来简化模式构建：

fn enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::seq(a : Exp, b : Exp) -> Exp
seq(Exp
a : enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp, Exp
b : enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp) -> enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp {
  match (Exp
a, Exp
b) {
    (Exp
Nil, _) | (_, Exp
Nil) => Exp
Nil
    (Exp
Eps, Exp
b) => Exp
b
    (Exp
a, Exp
Eps) => Exp
a
    (Exp
a, Exp
b) => (Exp, Exp) -> Exp
Seq(Exp
a, Exp
b)
  }
}

不过，Alt 的智能构造函数特别重要——它保证构造出的 Exp 符合 Brzozowski 原论文中的"相似性"标准化要求。两个正则表达式如果能通过以下规则相互转换，就被认为是相似的：

\begin{align} & A \mid \emptyset &&\rightarrow A \\ & A \mid B &&\rightarrow B \mid A \\ & A \mid (B \mid C) &&\rightarrow (A \mid B) \mid C \end{align}

因此，我们对 Alt 构造进行标准化，确保始终使用一致的结合律和选择顺序：

fn enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::alt(a : Exp, b : Exp) -> Exp
alt(Exp
a : enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp, Exp
b : enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp) -> enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp {
  match (Exp
a, Exp
b) {
    (Exp
Nil, Exp
b) => Exp
b
    (Exp
a, Exp
Nil) => Exp
a
    ((Exp, Exp) -> Exp
Alt(Exp
a, Exp
b), Exp
c) => Exp
a.fn Exp::alt(a : Exp, b : Exp) -> Exp
alt(Exp
b.fn Exp::alt(a : Exp, b : Exp) -> Exp
alt(Exp
c))
    (Exp
a, Exp
b) => {
      if Exp
a (Exp, Exp) -> Bool
automatically derived
== Exp
b {
        Exp
a
      } else if Exp
a (x : Exp, y : Exp) -> Bool
> Exp
b {
        (Exp, Exp) -> Exp
Alt(Exp
b, Exp
a)
      } else {
        (Exp, Exp) -> Exp
Alt(Exp
a, Exp
b)
      }
    }
  }
}

nullable 函数用于判断一个模式是否能够在不消费任何输入的情况下成功匹配（即匹配空字符串）：

fn enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::nullable(self : Exp) -> Bool
nullable(Exp
self : enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp) -> Bool
Bool {
  match Exp
self {
    Exp
Nil => false
    Exp
Eps => true
    (Char) -> Exp
Chr(_) => false
    (Exp, Exp) -> Exp
Alt(Exp
l, Exp
r) => Exp
l.fn Exp::nullable(self : Exp) -> Bool
nullable() (Bool, Bool) -> Bool
|| Exp
r.fn Exp::nullable(self : Exp) -> Bool
nullable()
    (Exp, Exp) -> Exp
Seq(Exp
l, Exp
r) => Exp
l.fn Exp::nullable(self : Exp) -> Bool
nullable() (Bool, Bool) -> Bool
&& Exp
r.fn Exp::nullable(self : Exp) -> Bool
nullable()
    (Exp) -> Exp
Rep(_) => true
  }
}

deriv 函数计算模式对于特定字符的导数，按照 Brzozowski 导数理论中定义的规则对模式进行变换。我们对规则进行了重新排列，使其与 deriv 函数的实现顺序保持一致：

\begin{align} D_{a} \emptyset &= \emptyset \\ D_{a} \epsilon &= \emptyset \\ D_{a} a &= \epsilon \\ D_{a} b &= \emptyset & \text{ for }(a \neq b) \\ D_{a} (P \mid Q) &= (D_{a} P) \mid (D_{a} Q) \\ D_{a} (P \cdot Q) &= (D_{a} P \cdot Q) \mid (\nu(P) \cdot D_{a} Q) \\ D_{a} (P\ast) &= D_{a} P \cdot P\ast \\ \end{align}

fn enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::deriv(self : Exp, c : Char) -> Exp
deriv(Exp
self : enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp, Char
c : Char
Char) -> enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp {
  match Exp
self {
    Exp
Nil => Exp
self
    Exp
Eps => Exp
Nil
    (Char) -> Exp
Chr(Char
d) if Char
d fn Eq::equal(self : Char, other : Char) -> Bool
Compares two characters for equality.
Parameters:

self : The first character to compare.
other : The second character to compare.
Returns true if both characters represent the same Unicode code point,
false otherwise.
Example:
let a = 'A'
let b = 'A'
let c = 'B'
inspect(a == b, content="true")
inspect(a == c, content="false")
== Char
c => Exp
Eps
    (Char) -> Exp
Chr(_) => Exp
Nil
    (Exp, Exp) -> Exp
Alt(Exp
l, Exp
r) => Exp
l.fn Exp::deriv(self : Exp, c : Char) -> Exp
deriv(Char
c).fn Exp::alt(a : Exp, b : Exp) -> Exp
alt(Exp
r.fn Exp::deriv(self : Exp, c : Char) -> Exp
deriv(Char
c))
    (Exp, Exp) -> Exp
Seq(Exp
l, Exp
r) => {
      let Exp
dl = Exp
l.fn Exp::deriv(self : Exp, c : Char) -> Exp
deriv(Char
c)
      if Exp
l.fn Exp::nullable(self : Exp) -> Bool
nullable() {
        Exp
dl.fn Exp::seq(a : Exp, b : Exp) -> Exp
seq(Exp
r).fn Exp::alt(a : Exp, b : Exp) -> Exp
alt(Exp
r.fn Exp::deriv(self : Exp, c : Char) -> Exp
deriv(Char
c))
      } else {
        Exp
dl.fn Exp::seq(a : Exp, b : Exp) -> Exp
seq(Exp
r)
      }
    }
    (Exp) -> Exp
Rep(Exp
e) => Exp
e.fn Exp::deriv(self : Exp, c : Char) -> Exp
deriv(Char
c).fn Exp::seq(a : Exp, b : Exp) -> Exp
seq(Exp
self)
  }
}

为了简化实现，我们这里只进行严格匹配，也就是说模式必须匹配整个输入字符串。因此，只有在处理完所有输入字符后，我们才检查最终模式的可空性：

fn enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::matches(self : Exp, s : String) -> Bool
matches(Exp
self : enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp, String
s : String
String) -> Bool
Bool {
  loop (Exp
self, String
s.fn String::view(self : String, start_offset? : Int, end_offset? : Int) -> StringView
Creates a View into a String.
Example
  let str = "Hello🤣🤣🤣"
  let view1 = str.view()
  inspect(view1, content=
   "Hello🤣🤣🤣"
  )
  let start_offset = str.offset_of_nth_char(1).unwrap()
  let end_offset = str.offset_of_nth_char(6).unwrap() // the second emoji
  let view2 = str.view(start_offset~, end_offset~)
  inspect(view2, content=
   "ello🤣"
  )
view()) {
    (Exp
Nil, _) => {
      return false
    }
    (Exp
e, []) => {
      return Exp
e.fn Exp::nullable(self : Exp) -> Bool
nullable()
    }
    (Exp
e, StringView
[Char
cStringView
, .. s]) => {
      continue (Exp
e.fn Exp::deriv(self : Exp, c : Char) -> Exp
deriv(Char
c), StringView
s)
    }
  }
}

虚拟机方法

虚拟机方法将正则表达式编译成简单虚拟机的字节码指令。这种方法把模式匹配问题转化为程序执行过程，虚拟机同时模拟非确定性有限自动机中所有可能的执行路径。

Ken Thompson 在 1968 年的经典论文中描述了一种将正则模式编译为 IBM 7094 机器代码的引擎。其关键思路是：通过维护多个执行线程来避免指数级回溯，这些线程同步地在输入中前进，每次处理一个字符，同时探索所有可能的匹配路径。

指令集与程序表示

该虚拟机基于四种基本指令运行，它们分别对应 NFA 的不同操作：

enum Ops {
  Ops
Done
  (Char) -> Ops
Char(Char
Char)
  (Int) -> Ops
Jump(Int
Int)
  (Int) -> Ops
Fork(Int
Int)
} derive(trait Show {
  output(Self, &Logger) -> Unit
  to_string(Self) -> String
}
Trait for types that can be converted to String
Show, trait ToJson {
  to_json(Self) -> Json
}
Trait for types that can be converted to Json
ToJson)

每条指令在 NFA 模拟中都有其特定作用：Done 标记匹配成功完成，对应 Thompson 原设计中的 match；Char(c) 消费输入字符 c 并跳转到下一条指令；Jump(addr) 无条件跳转至地址 addr，即 Thompson 的 jmp；Fork(addr) 创建两条执行路径——一条继续执行下一条指令，另一条跳转到 addr，对应 Thompson 的 split。

Fork 指令是处理模式非确定性的关键，比如选择和重复操作，这些情况下需要同时探索多条执行路径。这直接对应了 NFA 中的 ε-转换，即执行流可以在不消费输入的情况下发生分支。

我们定义了 Prg 类型，它封装了指令数组并提供便捷的方法来构建和操作字节码程序：

type Prg type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[enum Ops {
  Done
  Char(Char)
  Jump(Int)
  Fork(Int)
} derive(Show, ToJson)
Ops] derive(trait Show {
  output(Self, &Logger) -> Unit
  to_string(Self) -> String
}
Trait for types that can be converted to String
Show, trait ToJson {
  to_json(Self) -> Json
}
Trait for types that can be converted to Json
ToJson)

fn type Prg Array[Ops] derive(Show, ToJson)
Prg::fn Prg::push(self : Prg, inst : Ops) -> Unit
push(Prg
self : type Prg Array[Ops] derive(Show, ToJson)
Prg, Ops
inst : enum Ops {
  Done
  Char(Char)
  Jump(Int)
  Fork(Int)
} derive(Show, ToJson)
Ops) -> Unit
Unit {
  Prg
self.fn Prg::inner(self : Prg) -> Array[Ops]
Convert newtype to its underlying type, automatically derived.
inner().fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(Ops
inst)
}

fn type Prg Array[Ops] derive(Show, ToJson)
Prg::fn Prg::length(self : Prg) -> Int
length(Prg
self : type Prg Array[Ops] derive(Show, ToJson)
Prg) -> Int
Int {
  Prg
self.fn Prg::inner(self : Prg) -> Array[Ops]
Convert newtype to its underlying type, automatically derived.
inner().fn[T] Array::length(self : Array[T]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
let arr = [1, 2, 3]
inspect(arr.length(), content="3")
let empty : Array[Int] = []
inspect(empty.length(), content="0")
length()
}

fn type Prg Array[Ops] derive(Show, ToJson)
Prg::fn Prg::op_set(self : Prg, index : Int, inst : Ops) -> Unit
op_set(Prg
self : type Prg Array[Ops] derive(Show, ToJson)
Prg, Int
index : Int
Int, Ops
inst : enum Ops {
  Done
  Char(Char)
  Jump(Int)
  Fork(Int)
} derive(Show, ToJson)
Ops) -> Unit
Unit {
  Prg
selfArray[Ops]
Sets the element at the specified index in the array to a new value. The
original value at that index is overwritten.
Parameters:

array : The array to modify.
index : The position in the array where the value will be set.
value : The new value to assign at the specified index.
Throws an error if index is negative or greater than or equal to the length
of the array.
Example:
let arr = [1, 2, 3]
arr[1] = 42
inspect(arr, content="[1, 42, 3]")
.fn Prg::inner(self : Prg) -> Array[Ops]
Convert newtype to its underlying type, automatically derived.
innerArray[Ops]
Sets the element at the specified index in the array to a new value. The
original value at that index is overwritten.
Parameters:

array : The array to modify.
index : The position in the array where the value will be set.
value : The new value to assign at the specified index.
Throws an error if index is negative or greater than or equal to the length
of the array.
Example:
let arr = [1, 2, 3]
arr[1] = 42
inspect(arr, content="[1, 42, 3]")
()fn[T] Array::op_set(self : Array[T], index : Int, value : T) -> Unit
Sets the element at the specified index in the array to a new value. The
original value at that index is overwritten.
Parameters:

array : The array to modify.
index : The position in the array where the value will be set.
value : The new value to assign at the specified index.
Throws an error if index is negative or greater than or equal to the length
of the array.
Example:
let arr = [1, 2, 3]
arr[1] = 42
inspect(arr, content="[1, 42, 3]")
[index] = Ops
inst
}

AST 到字节码的编译

Prg::of_ast 函数采用标准的 NFA 构造技术，将 AST 模式转换为虚拟机指令：

Seq(a, b)：
```
code for a
code for b
```

Rep(a, None) (无界重复)：

    Fork L1, L2
L1: code for a
    Jump L1
L2:

Rep(a, Some(n)) (固定重复)：

code for a
code for a
... (n times) ...

Opt(a) (可选)：
```
    Fork L1, L2
L1: code for a
L2:
```

需要注意的是，Fork 构造器只接受一个地址参数，这是因为我们总是希望在 Fork 指令后继续执行下一条指令。

fn type Prg Array[Ops] derive(Show, ToJson)
Prg::fn Prg::of_ast(ast : Ast) -> Prg
of_ast(Ast
ast : enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast) -> type Prg Array[Ops] derive(Show, ToJson)
Prg {
  fn (Prg, Ast) -> Unit
compile(Prg
prog : type Prg Array[Ops] derive(Show, ToJson)
Prg, Ast
ast : enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast) -> Unit
Unit {
    match Ast
ast {
      (Char) -> Ast
Chr(Char
chr) => Prg
prog.fn Prg::push(self : Prg, inst : Ops) -> Unit
push((Char) -> Ops
Char(Char
chr))
      (Ast, Ast) -> Ast
Seq(Ast
l, Ast
r) => {
        (Prg, Ast) -> Unit
compile(Prg
prog, Ast
l)
        (Prg, Ast) -> Unit
compile(Prg
prog, Ast
r)
      }
      (Ast, Int?) -> Ast
Rep(Ast
e, Int?
None) => {
        let Int
fork = Prg
prog.fn Prg::length(self : Prg) -> Int
length()
        Prg
prog.fn Prg::push(self : Prg, inst : Ops) -> Unit
push((Int) -> Ops
Fork(0))
        (Prg, Ast) -> Unit
compile(Prg
prog, Ast
e)
        Prg
prog.fn Prg::push(self : Prg, inst : Ops) -> Unit
push((Int) -> Ops
Jump(Int
fork))
        Prg
progfn Prg::op_set(self : Prg, index : Int, inst : Ops) -> Unit
[fork] = (Int) -> Ops
Fork(Prg
prog.fn Prg::length(self : Prg) -> Int
length())
      }
      (Ast, Int?) -> Ast
Rep(Ast
e, (Int) -> Int?
Some(Int
n)) =>
        for _ in Int
0..<Int
n {
          (Prg, Ast) -> Unit
compile(Prg
prog, Ast
e)
        }
      (Ast) -> Ast
Opt(Ast
e) => {
        let Int
fork_inst = Prg
prog.fn Prg::length(self : Prg) -> Int
length()
        Prg
prog.fn Prg::push(self : Prg, inst : Ops) -> Unit
push((Int) -> Ops
Fork(0))
        (Prg, Ast) -> Unit
compile(Prg
prog, Ast
e)
        Prg
progfn Prg::op_set(self : Prg, index : Int, inst : Ops) -> Unit
[fork_inst] = (Int) -> Ops
Fork(Prg
prog.fn Prg::length(self : Prg) -> Int
length())
      }
    }
  }

  let Prg
prog : type Prg Array[Ops] derive(Show, ToJson)
Prg = []
  (Prg, Ast) -> Unit
compile(Prg
prog, Ast
ast)
  Prg
prog.fn Prg::push(self : Prg, inst : Ops) -> Unit
push(Ops
Done)
  Prg
prog
}

虚拟机执行循环

在 Rob Pike 的实现中，虚拟机会在输入字符串结束后再执行一轮来处理最终的接受状态。为了明确这个过程，我们的 matches 函数采用两阶段方法来实现核心的虚拟机执行循环：

阶段一：字符处理。对于每个输入字符，处理当前上下文中所有活跃的线程。如果 Char 指令匹配当前字符，就在下一个上下文中创建新线程。Jump 和 Fork 指令会立即在当前上下文中产生新线程。处理完所有线程后，交换上下文并继续处理下一个字符。

阶段二：最终接受判断。处理完所有输入后，检查剩余线程中是否有 Done 指令。同时处理那些不消费输入的 Jump/Fork 指令。如果有任何线程到达 Done 指令，就返回 true。

fn type Prg Array[Ops] derive(Show, ToJson)
Prg::fn Prg::matches(self : Prg, data : StringView) -> Bool
matches(Prg
self : type Prg Array[Ops] derive(Show, ToJson)
Prg, StringView
data : type StringView
@string.View) -> Bool
Bool {
  let (Array[Ops]) -> Prg
Prg(Array[Ops]
prog) = Prg
self
  let mut Ctx
curr = struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx::fn Ctx::new(length : Int) -> Ctx
new(Array[Ops]
prog.fn[T] Array::length(self : Array[T]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
let arr = [1, 2, 3]
inspect(arr.length(), content="3")
let empty : Array[Int] = []
inspect(empty.length(), content="0")
length())
  let mut Ctx
next = struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx::fn Ctx::new(length : Int) -> Ctx
new(Array[Ops]
prog.fn[T] Array::length(self : Array[T]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
let arr = [1, 2, 3]
inspect(arr.length(), content="3")
let empty : Array[Int] = []
inspect(empty.length(), content="0")
length())
  Ctx
curr.fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(0)
  for Char
c in StringView
data {
    while Ctx
curr.fn Ctx::pop(self : Ctx) -> Int?
pop() is (Int) -> Int?
Some(Int
pc) {
      match Array[Ops]
progfn[T] Array::op_get(self : Array[T], index : Int) -> T
Retrieves an element from the array at the specified index.
Parameters:

array : The array to get the element from.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Throws a panic if the index is negative or greater than or equal to the
length of the array.
Example:
let arr = [1, 2, 3]
inspect(arr[1], content="2")
[pc] {
        Ops
Done => ()
        (Char) -> Ops
Char(Char
char) if Char
char fn Eq::equal(self : Char, other : Char) -> Bool
Compares two characters for equality.
Parameters:

self : The first character to compare.
other : The second character to compare.
Returns true if both characters represent the same Unicode code point,
false otherwise.
Example:
let a = 'A'
let b = 'A'
let c = 'B'
inspect(a == b, content="true")
inspect(a == c, content="false")
== Char
c => {
          Ctx
next.fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(Int
pc fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ 1)
        }
        (Int) -> Ops
Jump(Int
jump) =>
          Ctx
curr.fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(Int
jump)
        (Int) -> Ops
Fork(Int
fork) => {
          Ctx
curr.fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(Int
fork)
          Ctx
curr.fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(Int
pc fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ 1)
        }
        _ => ()
      }
    }
    let Ctx
temp = Ctx
curr
    Ctx
curr = Ctx
next
    Ctx
next = Ctx
temp
    Ctx
next.fn Ctx::reset(self : Ctx) -> Unit
reset()
  }
  while Ctx
curr.fn Ctx::pop(self : Ctx) -> Int?
pop() is (Int) -> Int?
Some(Int
pc) {
    match Array[Ops]
progfn[T] Array::op_get(self : Array[T], index : Int) -> T
Retrieves an element from the array at the specified index.
Parameters:

array : The array to get the element from.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Throws a panic if the index is negative or greater than or equal to the
length of the array.
Example:
let arr = [1, 2, 3]
inspect(arr[1], content="2")
[pc] {
      Ops
Done => return true
      (Int) -> Ops
Jump(Int
x) => Ctx
curr.fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(Int
x)
      (Int) -> Ops
Fork(Int
x) => {
        Ctx
curr.fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(Int
x)
        Ctx
curr.fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(Int
pc fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ 1)
      }
      _ => ()
    }
  }
  false
}

在 Rob Pike 的原始博客中，他使用递归函数来处理 Fork 和 Jump 指令，以保证线程按优先级执行。而我们这里采用了类似栈的结构来管理所有执行线程，这样可以自然地维护线程优先级：

struct Ctx {
  @deque.Deque[Int]
deque : #alias(T, deprecated="`T` is deprecated, use `Deque` instead")
type @deque.Deque[A]
@deque.T[Int
Int]
  FixedArray[Bool]
visit : type FixedArray[A]
FixedArray[Bool
Bool]
}

fn struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx::fn Ctx::new(length : Int) -> Ctx
new(Int
length : Int
Int) -> struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx {
  { @deque.Deque[Int]
deque: fn[A] @moonbitlang/core/deque.new(capacity? : Int) -> @deque.Deque[A]
Creates a new empty deque with an optional initial capacity.
Parameters:

capacity : The initial capacity of the deque. If not specified, defaults
to 0 and will be automatically adjusted as elements are added.
Returns a new empty deque of type T[A] where A is the type of elements
the deque will hold.
Example
let dq : @deque.Deque[Int] = @deque.new()
inspect(dq.length(), content="0")
inspect(dq.capacity(), content="0")
let dq : @deque.Deque[Int] = @deque.new(capacity=10)
inspect(dq.length(), content="0")
inspect(dq.capacity(), content="10")
@deque.new(), FixedArray[Bool]
visit: type FixedArray[A]
FixedArray::fn[T] FixedArray::make(len : Int, init : T) -> FixedArray[T]
Creates a new fixed-size array with the specified length, initializing all
elements with the given value.
Parameters:

length : The length of the array to create. Must be non-negative.
initial_value : The value used to initialize all elements in the array.
Returns a new fixed-size array of type FixedArray[T] with length
elements, where each element is initialized to initial_value.
Throws a panic if length is negative.
Example:
let arr = FixedArray::make(3, 42)
inspect(arr[0], content="42")
inspect(arr.length(), content="3")
WARNING: A common pitfall is creating with the same initial value, for example:
let two_dimension_array = FixedArray::make(10, FixedArray::make(10, 0))
two_dimension_array[0][5] = 10
assert_eq(two_dimension_array[5][5], 10)
This is because all the cells reference to the same object (the FixedArray[Int] in this case).
One should use makei() instead which creates an object for each index.
make(Int
length, false) }
}

fn struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx::fn Ctx::add(self : Ctx, pc : Int) -> Unit
add(Ctx
self : struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx, Int
pc : Int
Int) -> Unit
Unit {
  if Bool
!Ctx
selfBool
.FixedArray[Bool]
visitfn[T] FixedArray::op_get(self : FixedArray[T], idx : Int) -> T
Retrieves an element at the specified index from a fixed-size array. This
function implements the array indexing operator [].
Parameters:

array : The fixed-size array to access.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Panics if the index is out of bounds.
Example:
let arr = FixedArray::make(3, 42)
inspect(arr[1], content="42")
[Bool
pc] {
    Ctx
self.@deque.Deque[Int]
deque.fn[A] @deque.Deque::push_back(self : @deque.Deque[A], value : A) -> Unit
Adds an element to the back of the deque.
If the deque is at capacity, it will be reallocated.
Example
  let dv = @deque.from_array([1, 2, 3, 4, 5])
  dv.push_back(6)
  assert_eq(dv.back(), Some(6))
push_back(Int
pc)
    Ctx
self.FixedArray[Bool]
visitfn[T] FixedArray::op_set(self : FixedArray[T], idx : Int, val : T) -> Unit
Sets the value at the specified index in a fixed-size array.
Parameters:

array : The fixed-size array to be modified.
index : The index at which to set the value. Must be non-negative and
less than the array's length.
value : The value to be set at the specified index.
Throws a runtime error if the index is out of bounds (less than 0 or greater
than or equal to the array's length).
Example:
let arr = FixedArray::make(3, 0)
arr.set(1, 42)
inspect(arr[1], content="42")
[pc] = true
  }
}

fn struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx::fn Ctx::pop(self : Ctx) -> Int?
pop(Ctx
self : struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx) -> Int
Int? {
  match Ctx
self.@deque.Deque[Int]
deque.fn[A] @deque.Deque::pop_back(self : @deque.Deque[A]) -> A?
Removes a back element from a deque and returns it, or None if it is empty.
Example
  let dv = @deque.from_array([1, 2, 3, 4, 5])
  assert_eq(dv.pop_back(), Some(5))
pop_back() {
    (Int) -> Int?
Some(Int
pc) => {
      Ctx
self.FixedArray[Bool]
visitfn[T] FixedArray::op_set(self : FixedArray[T], idx : Int, val : T) -> Unit
Sets the value at the specified index in a fixed-size array.
Parameters:

array : The fixed-size array to be modified.
index : The index at which to set the value. Must be non-negative and
less than the array's length.
value : The value to be set at the specified index.
Throws a runtime error if the index is out of bounds (less than 0 or greater
than or equal to the array's length).
Example:
let arr = FixedArray::make(3, 0)
arr.set(1, 42)
inspect(arr[1], content="42")
[pc] = false
      (Int) -> Int?
Some(Int
pc)
    }
    Int?
None => Int?
None
  }
}

fn struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx::fn Ctx::reset(self : Ctx) -> Unit
reset(Ctx
self : struct Ctx {
  deque: @deque.Deque[Int]
  visit: FixedArray[Bool]
}
Ctx) -> Unit
Unit {
  Ctx
self.@deque.Deque[Int]
deque.fn[A] @deque.Deque::clear(self : @deque.Deque[A]) -> Unit
Clears the deque, removing all values.
This method has no effect on the allocated capacity of the deque, only setting the length to 0.
Example
  let dv = @deque.from_array([1, 2, 3, 4, 5])
  dv.clear()
  inspect(dv.length(), content="0")
clear()
  Ctx
self.FixedArray[Bool]
visit.fn[T] FixedArray::fill(self : FixedArray[T], value : T, start? : Int, end? : Int) -> Unit
Fill the array with a given value.
This method fills all or part of a FixedArray with the given value.
Parameters

value: The value to fill the array with
start: The starting index (inclusive, default: 0)
end: The ending index (exclusive, optional)
If end is not provided, fills from start to the end of the array.
If start equals end, no elements are modified.
Panics

Panics if start is negative or greater than or equal to the array length
Panics if end is provided and is less than start or greater than array length
Does nothing if the array is empty
Example
// Fill entire array
let fa : FixedArray[Int] = [0, 0, 0, 0, 0]
fa.fill(3)
inspect(fa, content="[3, 3, 3, 3, 3]")

// Fill from index 1 to 3 (exclusive)
let fa2 : FixedArray[Int] = [0, 0, 0, 0, 0]
fa2.fill(9, start=1, end=3)
inspect(fa2, content="[0, 9, 9, 0, 0]")

// Fill from index 2 to end
let fa3 : FixedArray[String] = ["a", "b", "c", "d"]
fa3.fill("x", start=2)
inspect(
  fa3,
  content=(
    #|["a", "b", "x", "x"]
  ),
)
fill(false)
}

visit 数组用于过滤掉低优先级的重复线程。添加新线程时，我们先通过 visit 数组检查该线程是否已存在于 deque 中。如果已存在就直接丢弃；否则加入 deque 并标记为已访问。这个机制对于处理像 (a?)* 这样可能无限扩展的模式很重要，能够有效避免无限循环或指数级的线程爆炸。

基准测试与性能分析

我们通过一个对很多正则表达式实现都构成挑战的病理性案例来比较这两种方法：

test (@bench.Bench
b : #alias(T)
type @bench.Bench
@bench.T) {
  let Int
n = 15
  let String
txt = "a".fn String::repeat(self : String, n : Int) -> String
Returns a new string with self repeated n times.
repeat(Int
n)
  let Ast
chr = enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast::fn Ast::chr(chr : Char) -> Ast
chr('a')
  let Ast
ast : enum Ast {
  Chr(Char)
  Seq(Ast, Ast)
  Rep(Ast, Int?)
  Opt(Ast)
} derive(Show, ToJson, Hash, Eq)
Ast = Ast
chr.fn Ast::opt(self : Ast) -> Ast
opt().fn Ast::rep(self : Ast, n~ : Int) -> Ast
rep(Int
n~).fn Ast::seq(self : Ast, other : Ast) -> Ast
seq(Ast
chr.fn Ast::rep(self : Ast, n~ : Int) -> Ast
rep(Int
n~))
  let Exp
exp = enum Exp {
  Nil
  Eps
  Chr(Char)
  Alt(Exp, Exp)
  Seq(Exp, Exp)
  Rep(Exp)
} derive(Show, Hash, Eq, Compare, ToJson)
Exp::fn Exp::of_ast(ast : Ast) -> Exp
of_ast(Ast
ast)
  @bench.Bench
b.fn @bench.Bench::bench(self : @bench.Bench, name~ : String, f : () -> Unit, count? : UInt) -> Unit
Run a benchmark in batch mode
bench(String
name="derive", () => Exp
exp.fn Exp::matches(self : Exp, s : String) -> Bool
matches(String
txt) |> fn[T] ignore(t : T) -> Unit
Evaluates an expression and discards its result. This is useful when you want
to execute an expression for its side effects but don't care about its return
value, or when you want to explicitly indicate that a value is intentionally
unused.
Parameters:

value : The value to be ignored. Can be of any type.
Example:
let x = 42
ignore(x) // Explicitly ignore the value
let mut sum = 0
ignore([1, 2, 3].iter().each(x => sum = sum + x)) // Ignore the Unit return value of each()
ignore())
  let Prg
tvm = type Prg Array[Ops] derive(Show, ToJson)
Prg::fn Prg::of_ast(ast : Ast) -> Prg
of_ast(Ast
ast)
  @bench.Bench
b.fn @bench.Bench::bench(self : @bench.Bench, name~ : String, f : () -> Unit, count? : UInt) -> Unit
Run a benchmark in batch mode
bench(String
name="thompson", () => Prg
tvm.fn Prg::matches(self : Prg, data : StringView) -> Bool
matches(String
txt) |> fn[T] ignore(t : T) -> Unit
Evaluates an expression and discards its result. This is useful when you want
to execute an expression for its side effects but don't care about its return
value, or when you want to explicitly indicate that a value is intentionally
unused.
Parameters:

value : The value to be ignored. Can be of any type.
Example:
let x = 42
ignore(x) // Explicitly ignore the value
let mut sum = 0
ignore([1, 2, 3].iter().each(x => sum = sum + x)) // Ignore the Unit return value of each()
ignore())
}

模式 (a?){n}a{n} 是回溯引擎中典型的指数爆炸案例。这个模式有 n 种不同的方式来匹配 n 个 'a' 字符，在朴素的实现中会产生指数级的搜索空间。

name     time (mean ± σ)         range (min … max)
derive     41.78 µs ±   0.14 µs    41.61 µs …  42.13 µs  in 10 ×   2359 runs
thompson   12.79 µs ±   0.04 µs    12.74 µs …  12.84 µs  in 10 ×   7815 runs

从基准测试结果可以看出，在这种情况下虚拟机方法明显快于导数方法。导数方法需要频繁分配中间的正则表达式结构，带来了更高的开销和更慢的性能。相比之下，虚拟机执行的是一组固定的指令，一旦双端队列扩展到完整大小后，就很少需要分配新的结构了。

不过，导数方法在理论分析上更简洁。我们可以很容易地证明算法的终止性，因为需要计算的导数数量受到 AST 大小的限制，并且随着 deriv 函数的每次递归调用而严格递减。而虚拟机方法则不同，如果输入的 Prg 包含无限循环，程序可能永远不会终止，这就需要仔细处理线程优先级，以避免无限循环和线程数量的指数级增长。

prettyprinter：使用函数组合解决结构化数据打印问题

2025年9月3日 · 阅读需 9 分钟

结构化数据的打印是编程中常见的问题，尤其是在调试和日志记录时。如何展示复杂的数据结构，并能够根据屏幕宽度调整排版？例如，对于一个数组字面量 [a,b,c] , 我们希望在屏幕宽度足够时打印为一行，而在屏幕宽度不足时自动换行并缩进。传统的解决方案往往依赖于手动处理字符串拼接和维护缩进状态，这样的方式不仅繁琐，而且容易出错。

本篇文章将介绍一种基于函数组合的实用方案——prettyprinter的实现。Prettyprinter 向用户提供了一系列函数，这些函数能够组合成一个描述了打印方式的Doc原语。然后，根据宽度配置和Doc原语生成最终的字符串。函数组合的思路使得用户能够复用已有的代码，声明式地实现数据结构的打印。

SimpleDoc 原语

我们先定义一个SimpleDoc表示4个最简单的原语，来处理最基本的字符串拼接和换行。

enum SimpleDoc {
  SimpleDoc
Empty
  SimpleDoc
Line
  (String) -> SimpleDoc
Text(String
String)
  (SimpleDoc, SimpleDoc) -> SimpleDoc
Cat(enum SimpleDoc {
  Empty
  Line
  Text(String)
  Cat(SimpleDoc, SimpleDoc)
}
SimpleDoc, enum SimpleDoc {
  Empty
  Line
  Text(String)
  Cat(SimpleDoc, SimpleDoc)
}
SimpleDoc)
}

Empty: 表示空字符串
Line：表示换行
Text(String): 表示一个不包含换行的文本片段
Cat(SimpleDoc, SimpleDoc): 按顺序组合两个 SimpleDoc

按照上面每个原语的定义，我们可以实现一个简单的渲染函数：这个函数使用一个栈来保存待处理的SimpleDoc，逐个将它们转换为字符串。

fn enum SimpleDoc {
  Empty
  Line
  Text(String)
  Cat(SimpleDoc, SimpleDoc)
}
SimpleDoc::fn SimpleDoc::render(doc : SimpleDoc) -> String
render(SimpleDoc
doc : enum SimpleDoc {
  Empty
  Line
  Text(String)
  Cat(SimpleDoc, SimpleDoc)
}
SimpleDoc) -> String
String {
  let StringBuilder
buf = type StringBuilder
StringBuilder::fn StringBuilder::new(size_hint? : Int) -> StringBuilder
Creates a new string builder with an optional initial capacity hint.
Parameters:

size_hint : An optional initial capacity hint for the internal buffer. If
less than 1, a minimum capacity of 1 is used. Defaults to 0. It is the size of bytes,
not the size of characters. size_hint may be ignored on some platforms, JS for example.
Returns a new StringBuilder instance with the specified initial capacity.
new()
  let Array[SimpleDoc]
stack = [SimpleDoc
doc]
  while Array[SimpleDoc]
stack.fn[T] Array::pop(self : Array[T]) -> T?
Removes the last element from an array and returns it, or None if it is empty.
Example
  let v = [1, 2, 3]
  assert_eq(v.pop(), Some(3))
  assert_eq(v, [1, 2])
pop() is (SimpleDoc) -> SimpleDoc?
Some(SimpleDoc
doc) {
    match SimpleDoc
doc {
      SimpleDoc
Empty => ()
      SimpleDoc
Line => {
        StringBuilder
buf..fn Logger::write_string(self : StringBuilder, str : String) -> Unit
Writes a string to the StringBuilder.
write_string("\n")
      }
      (String) -> SimpleDoc
Text(String
text) => {
        StringBuilder
buf.fn Logger::write_string(self : StringBuilder, str : String) -> Unit
Writes a string to the StringBuilder.
write_string(String
text)
      }
      (SimpleDoc, SimpleDoc) -> SimpleDoc
Cat(SimpleDoc
left, SimpleDoc
right) =>
        Array[SimpleDoc]
stack..fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(SimpleDoc
right)..fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(SimpleDoc
left)
    }
  }
  StringBuilder
buf.fn StringBuilder::to_string(self : StringBuilder) -> String
Returns the current content of the StringBuilder as a string.
to_string()
}

编写测试，可以看到SimpleDoc的表达能力和 String 相当: Empty 相当于 "" ， Line 相当于 "\n" , Text("a") 相当于 "a" ， Cat(Text("a"), Text("b")) 相当于 "a" + "b" 。

test "simple doc" {
  let SimpleDoc
doc : enum SimpleDoc {
  Empty
  Line
  Text(String)
  Cat(SimpleDoc, SimpleDoc)
}
SimpleDoc = (SimpleDoc, SimpleDoc) -> SimpleDoc
Cat((String) -> SimpleDoc
Text("hello"), (SimpleDoc, SimpleDoc) -> SimpleDoc
Cat(SimpleDoc
Line, (String) -> SimpleDoc
Text("world")))
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    SimpleDoc
doc.fn SimpleDoc::render(doc : SimpleDoc) -> String
render(),
    String
content=(
      #|hello
      #|world
    ),
  )
}

目前它还和String一样无法方便地处理缩进和排版切换。不过，只要再添加三个原语就可以解决这些问题。

ExtendDoc：Nest, Choice, Group

接下来我们在SimpleDoc的基础上，添加三个新的原语Nest、Choice、Group来处理更复杂的打印需求。

enum ExtendDoc {
  ExtendDoc
Empty
  ExtendDoc
Line
  (String) -> ExtendDoc
Text(String
String)
  (ExtendDoc, ExtendDoc) -> ExtendDoc
Cat(enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc, enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc)
  (Int, ExtendDoc) -> ExtendDoc
Nest(Int
Int,enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc)
  (ExtendDoc, ExtendDoc) -> ExtendDoc
Choice(enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc, enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc)
  (ExtendDoc) -> ExtendDoc
Group(enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc)
}

Nest Nest(Int, ExtendDoc) 用于处理缩进。第一个参数表示缩进的空格数，第二个参数表示内部的 ExtendDoc 。当内部的 ExtendDoc 包含 Line 时，render函数将在打印换行的同时追加相应数量的空格。 Nest 嵌套使用时缩进会累加。
Choice Choice(ExtendDoc, ExtendDoc) 保存了两种打印方式。通常第一个参数表示不包含换行更紧凑的布局，第二个参数则是包含 Line 的布局。当render在紧凑模式时，使用第一个布局，否则使用第二个。
Group Group(ExtendDoc) 将ExtendDoc分组，并根据 ExtendDoc 的长度和剩余的空间切换打印 ExtendDoc 时的模式。如果剩余空间足够，则在紧凑模式下打印，否则使用包含换行的布局。

计算所需空间

Group的实现需要计算 ExtendDoc 的空间需求，以便决定是否使用紧凑模式。我们可以为 ExtendDoc 添加一个 space() 方法来计算每个布局片段所需的空间。

let Int
max_space = 9999

fn enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc::fn ExtendDoc::space(self : ExtendDoc) -> Int
space(ExtendDoc
self : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
Self) -> Int
Int {
  match ExtendDoc
self {
    ExtendDoc
Empty => 0
    ExtendDoc
Line => let max_space : Int
max_space
    (String) -> ExtendDoc
Text(String
str) => String
str.fn String::length(self : String) -> Int
Returns the number of UTF-16 code units in the string. Note that this is not
necessarily equal to the number of Unicode characters (code points) in the
string, as some characters may be represented by multiple UTF-16 code units.
Parameters:

string : The string whose length is to be determined.
Returns the number of UTF-16 code units in the string.
Example:
inspect("hello".length(), content="5")
inspect("🤣".length(), content="2") // Emoji uses two UTF-16 code units
inspect("".length(), content="0") // Empty string
length()
    (ExtendDoc, ExtendDoc) -> ExtendDoc
Cat(ExtendDoc
a, ExtendDoc
b) => ExtendDoc
a.fn ExtendDoc::space(self : ExtendDoc) -> Int
space() fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ ExtendDoc
b.fn ExtendDoc::space(self : ExtendDoc) -> Int
space()
    (Int, ExtendDoc) -> ExtendDoc
Nest(_, ExtendDoc
a) | (ExtendDoc, ExtendDoc) -> ExtendDoc
Choice(ExtendDoc
a, _) | (ExtendDoc) -> ExtendDoc
Group(ExtendDoc
a) => ExtendDoc
a.fn ExtendDoc::space(self : ExtendDoc) -> Int
space()
  }
}

对于 Line , 我们假设它总是需要占用无限大的空间。这样如果 Group 内包含 Line，能够保证render处理内部的 ExtendDoc 时不会进入紧凑模式。

实现 ExtendDoc::render

我们在SimpleDoc::render的基础上实现 ExtendDoc::render 。 render在打印完一个子结构后，继续打印后续的结构需要退回到原先的缩进层级，因此需要在stack中额外保存每个待打印的ExtendDoc的两个状态：缩进和是否在紧凑模式。我们还需要维护了一个在render过程中更新的 column 变量，表示当前行的已经使用的字符数，以计算当前行所剩的空间。另外，函数增加了额外的width参数，表示每行的最大宽度限制。

fn enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc::fn ExtendDoc::render(doc : ExtendDoc, width? : Int) -> String
render(ExtendDoc
doc : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc, Int
width~ : Int
Int = 80) -> String
String {
  let StringBuilder
buf = type StringBuilder
StringBuilder::fn StringBuilder::new(size_hint? : Int) -> StringBuilder
Creates a new string builder with an optional initial capacity hint.
Parameters:

size_hint : An optional initial capacity hint for the internal buffer. If
less than 1, a minimum capacity of 1 is used. Defaults to 0. It is the size of bytes,
not the size of characters. size_hint may be ignored on some platforms, JS for example.
Returns a new StringBuilder instance with the specified initial capacity.
new()
  let Array[(Int, Bool, ExtendDoc)]
stack = [(0, false, ExtendDoc
doc)] // 默认不缩进，非紧凑模式
  let mut Int
column = 0
  while Array[(Int, Bool, ExtendDoc)]
stack.fn[T] Array::pop(self : Array[T]) -> T?
Removes the last element from an array and returns it, or None if it is empty.
Example
  let v = [1, 2, 3]
  assert_eq(v.pop(), Some(3))
  assert_eq(v, [1, 2])
pop() is ((Int, Bool, ExtendDoc)) -> (Int, Bool, ExtendDoc)?
Some((Int
indent, Bool
fit, ExtendDoc
doc)) {
    match ExtendDoc
doc {
      ExtendDoc
Empty => ()
      ExtendDoc
Line => {
        StringBuilder
buf..fn Logger::write_string(self : StringBuilder, str : String) -> Unit
Writes a string to the StringBuilder.
write_string("\n")
        // 在换行后打印需要的缩进
        for _ in Int
0..<Int
indent {
          StringBuilder
buf.fn Logger::write_string(self : StringBuilder, str : String) -> Unit
Writes a string to the StringBuilder.
write_string(" ")
        }
        // 重置当前行的字符数
        Int
column = Int
indent
      }
      (String) -> ExtendDoc
Text(String
text) => {
        StringBuilder
buf.fn Logger::write_string(self : StringBuilder, str : String) -> Unit
Writes a string to the StringBuilder.
write_string(String
text)
        // 更新当前行的字符数
        Int
column fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+= String
text.fn String::length(self : String) -> Int
Returns the number of UTF-16 code units in the string. Note that this is not
necessarily equal to the number of Unicode characters (code points) in the
string, as some characters may be represented by multiple UTF-16 code units.
Parameters:

string : The string whose length is to be determined.
Returns the number of UTF-16 code units in the string.
Example:
inspect("hello".length(), content="5")
inspect("🤣".length(), content="2") // Emoji uses two UTF-16 code units
inspect("".length(), content="0") // Empty string
length()
      }
      (ExtendDoc, ExtendDoc) -> ExtendDoc
Cat(ExtendDoc
left, ExtendDoc
right) =>
        Array[(Int, Bool, ExtendDoc)]
stack..fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push((Int
indent, Bool
fit, ExtendDoc
right))..fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push((Int
indent, Bool
fit, ExtendDoc
left))
      (Int, ExtendDoc) -> ExtendDoc
Nest(Int
n, ExtendDoc
doc) => Array[(Int, Bool, ExtendDoc)]
stack..fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push((Int
indent fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ Int
n, Bool
fit, ExtendDoc
doc)) // 增加缩进
      (ExtendDoc, ExtendDoc) -> ExtendDoc
Choice(ExtendDoc
a, ExtendDoc
b) =>
        Array[(Int, Bool, ExtendDoc)]
stack.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(if Bool
fit { (Int
indent, Bool
fit, ExtendDoc
a) } else { (Int
indent, Bool
fit, ExtendDoc
b) })
      (ExtendDoc) -> ExtendDoc
Group(ExtendDoc
doc) => {
        // 如果已经在紧凑模式下，直接使用紧凑布局。如果不在紧凑模式下，但是要打印的内容可以放入当前行，则进入紧凑模式。
        let Bool
fit = Bool
fit (Bool, Bool) -> Bool
|| Int
column fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ ExtendDoc
doc.fn ExtendDoc::space(self : ExtendDoc) -> Int
space() fn Compare::op_le(x : Int, y : Int) -> Bool
<= Int
width
        Array[(Int, Bool, ExtendDoc)]
stack.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push((Int
indent, Bool
fit, ExtendDoc
doc))
      }
    }
  }
  StringBuilder
buf.fn StringBuilder::to_string(self : StringBuilder) -> String
Returns the current content of the StringBuilder as a string.
to_string()
}

下面我们尝试用 ExtendDoc 描述一个 (expr) ，并在不同的宽度配置下打印它：

let ExtendDoc
softline : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (ExtendDoc, ExtendDoc) -> ExtendDoc
Choice(ExtendDoc
Empty, ExtendDoc
Line)

impl trait Add {
  add(Self, Self) -> Self
  op_add(Self, Self) -> Self
}
types implementing this trait can use the + operator
Add for enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc with fn Add::op_add(a : ExtendDoc, b : ExtendDoc) -> ExtendDoc
op_add(ExtendDoc
a, ExtendDoc
b) {
  (ExtendDoc, ExtendDoc) -> ExtendDoc
Cat(ExtendDoc
a, ExtendDoc
b)
}

test "tuple" {
  let ExtendDoc
tuple : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (ExtendDoc) -> ExtendDoc
Group(
    (String) -> ExtendDoc
Text("(") (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ (Int, ExtendDoc) -> ExtendDoc
Nest(2, let softline : ExtendDoc
softline (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ (String) -> ExtendDoc
Text("expr")) (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let softline : ExtendDoc
softline (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ (String) -> ExtendDoc
Text(")"),
  )
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(ExtendDoc
tuple.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=40), String
content="(expr)")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    ExtendDoc
tuple.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=5),
    String
content=(
      #|(
      #|  expr
      #|)
    ),
  )
}

我们先通过组合Empty和Line的方式定义了一个在紧凑模式下不换行的 softline 。render默认以非紧凑模式开始打印，所以我们需要用 Group 将整个表达式包裹起来。这样在宽度足够时，整个表达式会打印为一行，而在宽度不足时会自动换行并缩进。为了减少嵌套的括号，改善可读性，这里给 ExtendDoc 重载了 + 运算符。

组合函数

在prettyprinter的实践中，用户更多地会使用在 ExtendDoc 原语基础之上组合出的函数——例如之前使用过的 softline 。下面将介绍一些实用的函数，帮助我们解决结构化打印的问题。

softline & softbreak

let ExtendDoc
softbreak : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (ExtendDoc, ExtendDoc) -> ExtendDoc
Choice((String) -> ExtendDoc
Text(" "), ExtendDoc
Line)

和 softline 类似，不同的是在紧凑模式下它会加入额外的空格。注意在同一层 Group 中，每个 Choice 都会一致选择紧凑或非紧凑模式。

let ExtendDoc
abc : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (String) -> ExtendDoc
Text("abc")

let ExtendDoc
def : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (String) -> ExtendDoc
Text("def")

let ExtendDoc
ghi : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (String) -> ExtendDoc
Text("ghi")

test "softbreak" {
  let ExtendDoc
doc : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (ExtendDoc) -> ExtendDoc
Group(let abc : ExtendDoc
abc (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let softbreak : ExtendDoc
softbreak (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let def : ExtendDoc
def (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let softbreak : ExtendDoc
softbreak (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let ghi : ExtendDoc
ghi)
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(ExtendDoc
doc.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=20), String
content="abc def ghi")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    ExtendDoc
doc.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=10),
    String
content=(
      #|abc
      #|def
      #|ghi
    ),
  )
}

autoline & autobreak

let ExtendDoc
autoline : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (ExtendDoc) -> ExtendDoc
Group(let softline : ExtendDoc
softline)

let ExtendDoc
autobreak : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (ExtendDoc) -> ExtendDoc
Group(let softbreak : ExtendDoc
softbreak)

autoline 和 autobreak 实现一种类似于文字编辑器的排版：尽可能多地将内容放进一行内，溢出则换行。

test {
  let ExtendDoc
doc : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (ExtendDoc) -> ExtendDoc
Group(
    let abc : ExtendDoc
abc (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let autobreak : ExtendDoc
autobreak (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let def : ExtendDoc
def (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let autobreak : ExtendDoc
autobreak (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let ghi : ExtendDoc
ghi,
  )
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(ExtendDoc
doc.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=10), String
content="abc def ghi")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    ExtendDoc
doc.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=5),
    String
content=(
      #|abc def
      #|ghi
    ),
  )
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    ExtendDoc
doc.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=3),
    String
content=(
      #|abc
      #|def
      #|ghi
    ),
  )
}

sepby

fn fn sepby(xs : Array[ExtendDoc], sep : ExtendDoc) -> ExtendDoc
sepby(Array[ExtendDoc]
xs : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc], ExtendDoc
sep : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc) -> enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc {
  match Array[ExtendDoc]
xs {
    [] => ExtendDoc
Empty
    Array[ExtendDoc]
[ExtendDoc
xArray[ExtendDoc]
, .. xs] => ArrayView[ExtendDoc]
xs.fn[A, B] ArrayView::fold(self : ArrayView[A], init~ : B, f : (B, A) -> B raise?) -> B raise?
Fold out values from an ArrayView according to certain rules.
Example
  let sum = [1, 2, 3, 4, 5][:].fold(init=0, (sum, elem) => sum + elem)
  inspect(sum, content="15")
fold(ExtendDoc
init=ExtendDoc
x, (ExtendDoc
a, ExtendDoc
b) => ExtendDoc
a (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ ExtendDoc
sep (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ ExtendDoc
b)
  }
}

sepby会在ExtendDoc之间插入分隔符sep。

let ExtendDoc
comma : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc = (String) -> ExtendDoc
Text(",")
test {
  let ExtendDoc
layout = (ExtendDoc) -> ExtendDoc
Group(fn sepby(xs : Array[ExtendDoc], sep : ExtendDoc) -> ExtendDoc
sepby([let abc : ExtendDoc
abc, let def : ExtendDoc
def, let ghi : ExtendDoc
ghi], let comma : ExtendDoc
comma (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let softbreak : ExtendDoc
softbreak))
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(ExtendDoc
layout.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=40), String
content="abc, def, ghi")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    ExtendDoc
layout.fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=10),
    String
content=(
      #|abc,
      #|def,
      #|ghi

    ),
  )
}

surround

fn fn surround(m : ExtendDoc, l : ExtendDoc, r : ExtendDoc) -> ExtendDoc
surround(ExtendDoc
m : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc, ExtendDoc
l : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc, ExtendDoc
r : enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc) -> enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc {
  ExtendDoc
l (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ ExtendDoc
m (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ ExtendDoc
r
}

surround 用于在 ExtendDoc 的两侧添加括号或其他分隔符。

test {
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(fn surround(m : ExtendDoc, l : ExtendDoc, r : ExtendDoc) -> ExtendDoc
surround(let abc : ExtendDoc
abc, (String) -> ExtendDoc
Text("("), (String) -> ExtendDoc
Text(")")).fn ExtendDoc::render(doc : ExtendDoc, width? : Int) -> String
render(), String
content="(abc)")
}

打印Json

利用上面定义的函数，我们可以实现一个打印Json的函数。这个函数将递归地处理Json的每个元素，生成相应的布局。

fn fn pretty(x : Json) -> ExtendDoc
pretty(Json
x : enum Json {
  Null
  True
  False
  Number(Double, repr~ : String?)
  String(String)
  Array(Array[Json])
  Object(Map[String, Json])
}
Json) -> enum ExtendDoc {
  Empty
  Line
  Text(String)
  Cat(ExtendDoc, ExtendDoc)
  Nest(Int, ExtendDoc)
  Choice(ExtendDoc, ExtendDoc)
  Group(ExtendDoc)
}
ExtendDoc {
  fn (Array[ExtendDoc], ExtendDoc, ExtendDoc) -> ExtendDoc
comma_list(Array[ExtendDoc]
xs, ExtendDoc
l, ExtendDoc
r) {
    ((Int, ExtendDoc) -> ExtendDoc
Nest(2, let softline : ExtendDoc
softline (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ fn sepby(xs : Array[ExtendDoc], sep : ExtendDoc) -> ExtendDoc
sepby(Array[ExtendDoc]
xs, let comma : ExtendDoc
comma (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let softbreak : ExtendDoc
softbreak)) (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ let softline : ExtendDoc
softline)
    |> fn surround(m : ExtendDoc, l : ExtendDoc, r : ExtendDoc) -> ExtendDoc
surround(ExtendDoc
l, ExtendDoc
r)
    |> (ExtendDoc) -> ExtendDoc
Group
  }

  match Json
x {
    (Array[Json]) -> Json
Array(Array[Json]
elems) => {
      let Array[ExtendDoc]
elems = Array[Json]
elems.fn[T] Array::iter(self : Array[T]) -> Iter[T]
Creates an iterator over the elements of the array.
Parameters:

array : The array to create an iterator from.
Returns an iterator that yields each element of the array in order.
Example:
let arr = [1, 2, 3]
let mut sum = 0
arr.iter().each(x => sum = sum + x)
inspect(sum, content="6")
iter().fn[T, R] Iter::map(self : Iter[T], f : (T) -> R) -> Iter[R]
Transforms the elements of the iterator using a mapping function.
Type Parameters

T: The type of the elements in the iterator.
R: The type of the transformed elements.
Arguments

self - The input iterator.
f - The mapping function that transforms each element of the iterator.
Returns
A new iterator that contains the transformed elements.
map(fn pretty(x : Json) -> ExtendDoc
pretty).fn[T] Iter::collect(self : Iter[T]) -> Array[T]
Collects the elements of the iterator into an array.
collect()
      (Array[ExtendDoc], ExtendDoc, ExtendDoc) -> ExtendDoc
comma_list(Array[ExtendDoc]
elems, (String) -> ExtendDoc
Text("["), (String) -> ExtendDoc
Text("]"))
    }
    (Map[String, Json]) -> Json
Object(Map[String, Json]
pairs) => {
      let Array[ExtendDoc]
pairs = Map[String, Json]
pairs
        .fn[K, V] Map::iter(self : Map[K, V]) -> Iter[(K, V)]
Returns the iterator of the hash map, provide elements in the order of insertion.
iter()
        .fn[T, R] Iter::map(self : Iter[T], f : (T) -> R) -> Iter[R]
Transforms the elements of the iterator using a mapping function.
Type Parameters

T: The type of the elements in the iterator.
R: The type of the transformed elements.
Arguments

self - The input iterator.
f - The mapping function that transforms each element of the iterator.
Returns
A new iterator that contains the transformed elements.
map((String, Json)
p => (ExtendDoc) -> ExtendDoc
Group((String) -> ExtendDoc
Text((String, Json)
p.String
0.fn String::escape(self : String) -> String
Returns a valid MoonBit string literal representation of a string,
add quotes and escape special characters.
Examples
  let str = "Hello \n"
  inspect(str.to_string(), content="Hello \n")
  inspect(str.escape(), content="\"Hello \\n\"")
escape()) (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ (String) -> ExtendDoc
Text(": ") (self : ExtendDoc, other : ExtendDoc) -> ExtendDoc
+ fn pretty(x : Json) -> ExtendDoc
pretty((String, Json)
p.Json
1)))
        .fn[T] Iter::collect(self : Iter[T]) -> Array[T]
Collects the elements of the iterator into an array.
collect()
      (Array[ExtendDoc], ExtendDoc, ExtendDoc) -> ExtendDoc
comma_list(Array[ExtendDoc]
pairs, (String) -> ExtendDoc
Text("{"), (String) -> ExtendDoc
Text("}"))
    }
    (String) -> Json
String(String
s) => (String) -> ExtendDoc
Text(String
s.fn String::escape(self : String) -> String
Returns a valid MoonBit string literal representation of a string,
add quotes and escape special characters.
Examples
  let str = "Hello \n"
  inspect(str.to_string(), content="Hello \n")
  inspect(str.escape(), content="\"Hello \\n\"")
escape())
    (Double, repr~ : String?) -> Json
Number(Double
i) => (String) -> ExtendDoc
Text(Double
i.fn Double::to_string(self : Double) -> String
Converts a double-precision floating-point number to its string
representation.
Parameters:

self: The double-precision floating-point number to be converted.
Returns a string representation of the double-precision floating-point
number.
Example:
inspect(42.0.to_string(), content="42")
inspect(3.14159.to_string(), content="3.14159")
inspect((-0.0).to_string(), content="0")
inspect(@double.not_a_number.to_string(), content="NaN")
to_string())
    Json
False => (String) -> ExtendDoc
Text("false")
    Json
True => (String) -> ExtendDoc
Text("true")
    Json
Null => (String) -> ExtendDoc
Text("null")
  }
}

可以看到在不同的打印宽度下，Json的排版会自动调整。

test {
  let Json
json : enum Json {
  Null
  True
  False
  Number(Double, repr~ : String?)
  String(String)
  Array(Array[Json])
  Object(Map[String, Json])
}
Json = {
    "key1": "string",
    "key2": [12345, 67890],
    "key3": [
      { "field1": 1, "field2": 2 },
      { "field1": 1, "field2": 2 },
      { "field1": [1, 2], "field2": 2 },
    ],
  }
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    fn pretty(x : Json) -> ExtendDoc
pretty(Json
json).fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=80),
    String
content=(
      #|{
      #|  "key1": "string",
      #|  "key2": [12345, 67890],
      #|  "key3": [
      #|    {"field1": 1, "field2": 2},
      #|    {"field1": 1, "field2": 2},
      #|    {"field1": [1, 2], "field2": 2}
      #|  ]
      #|}
    ),
  )
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    fn pretty(x : Json) -> ExtendDoc
pretty(Json
json).fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=30),
    String
content=(
      #|{
      #|  "key1": "string",
      #|  "key2": [12345, 67890],
      #|  "key3": [
      #|    {"field1": 1, "field2": 2},
      #|    {"field1": 1, "field2": 2},
      #|    {
      #|      "field1": [1, 2],
      #|      "field2": 2
      #|    }
      #|  ]
      #|}
    ),
  )
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(
    fn pretty(x : Json) -> ExtendDoc
pretty(Json
json).fn ExtendDoc::render(doc : ExtendDoc, width~ : Int) -> String
render(Int
width=20),
    String
content=(
      #|{
      #|  "key1": "string",
      #|  "key2": [
      #|    12345,
      #|    67890
      #|  ],
      #|  "key3": [
      #|    {
      #|      "field1": 1,
      #|      "field2": 2
      #|    },
      #|    {
      #|      "field1": 1,
      #|      "field2": 2
      #|    },
      #|    {
      #|      "field1": [
      #|        1,
      #|        2
      #|      ],
      #|      "field2": 2
      #|    }
      #|  ]
      #|}
    ),
  )
}

总结

本文介绍了如何简单实现一个prettyprinter，使用函数组合的方式来处理结构化数据的打印。通过定义一系列原语和组合函数，我们可以灵活地控制打印格式，并根据屏幕宽度自动调整布局。

当前的实现还可以进一步优化，例如通过记忆化space的计算来提高性能。ExtendDoc::render函数可以增加一个ribbon参数，分别统计当前行的空格和其他文本字数，并且在Group的紧凑模式判断中增加额外的条件，来控制每行的信息密度。另外，还可以增加更多的原语来实现悬挂缩进、最小换行数量等功能。对于更多的设计和实现细节感兴趣的读者，可以参考A prettier printer - Philip Wadler以及Haskell、OCaml等语言的prettyprinter实现。

Mini-adapton: 用 MoonBit 实现增量计算

2025年8月27日 · 阅读需 10 分钟

介绍

让我们先用一个类似 excel 的例子感受一下增量计算长什么样子. 首先, 定义一个这样的依赖图:

在这个图中, t1 的值通过 n1 + n2 计算得到, t2 的值通过 t1 + n3 计算得到.

当我们想得到 t2 的值时, 该图定义的计算将被执行: 首先通过 n1 + n2 算出 t1, 再通过 t1 + n3 算出 t2. 这个过程和非增量计算是相同的.

但当我们开始改变n1, n2 或 n3 的值时, 事情就不一样了. 比如说我们想将 n1 和 n2 的值互换, 再得到 t2 的值. 在非增量计算中, t1 和 t2 都将被重新计算一遍, 但实际上 t2 是不需要被重新计算的, 因为它依赖的两个值 t1 和 n3 都没有改变 (将 n1 和 n2 的值互换不会改变 t1 的值).

下面的代码实现了我们刚刚举的例子. 我们使用 Cell::new 来定义 n1, n2 和 n3 这些不需要计算的东西, 使用 Thunk::new 来定义 t1 和 t2 这样需要计算的东西.

test {
  // a counter to record the times of t2's computation
  let mut Int
cnt = 0
  // start define the graph
  let Cell[Int]
n1 = struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::fn[A : Eq] Cell::new(value : A) -> Cell[A]
new(1)
  let Cell[Int]
n2 = struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::fn[A : Eq] Cell::new(value : A) -> Cell[A]
new(2)
  let Cell[Int]
n3 = struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::fn[A : Eq] Cell::new(value : A) -> Cell[A]
new(3)
  let Thunk[Int]
t1 = struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::fn[A : Eq] Thunk::new(thunk : () -> A) -> Thunk[A]
new(fn() {
    Cell[Int]
n1.fn[A] Cell::get(self : Cell[A]) -> A
get() fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ Cell[Int]
n2.fn[A] Cell::get(self : Cell[A]) -> A
get()
  })
  let Thunk[Int]
t2 = struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::fn[A : Eq] Thunk::new(thunk : () -> A) -> Thunk[A]
new(fn() {
    Int
cnt fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+= 1
    Thunk[Int]
t1.fn[A : Eq] Thunk::get(self : Thunk[A]) -> A
get() fn Add::add(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
inspect(42 + 1, content="43")
inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ Cell[Int]
n3.fn[A] Cell::get(self : Cell[A]) -> A
get()
  })
  // get the value of t2
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Thunk[Int]
t2.fn[A : Eq] Thunk::get(self : Thunk[A]) -> A
get(), String
content="6")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Int
cnt, String
content="1")
  // swap value of n1 and n2
  Cell[Int]
n1.fn[A : Eq] Cell::set(self : Cell[A], new_value : A) -> Unit
set(2)
  Cell[Int]
n2.fn[A : Eq] Cell::set(self : Cell[A], new_value : A) -> Unit
set(1)
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Thunk[Int]
t2.fn[A : Eq] Thunk::get(self : Thunk[A]) -> A
get(), String
content="6")
  // t2 does not recompute
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Int
cnt, String
content="1")
}

在这篇文章中, 我们将介绍如何在 MoonBit 中实现一个增量计算库. 这个库的 API 就是我们上面例子中出现的那些:

Cell::new
Cell::get
Cell::set
Thunk::new
Thunk::get

问题分析和解法

要实现这个库, 我们主要有三个问题需要解决:

如何在运行时构建依赖图

作为一个使用 MoonBit 实现的库, 没有简单方法让我们可以静态地构建依赖图, 因为 MoonBit 目前还不支持任何元编程的机制. 因此我们需要动态地把依赖图构建出来. 事实上, 我们关心的只是哪些 thunk 或 cell 被另一个 thunk 依赖了, 所以一个不错的构建依赖图的时机就是在用户调用 Thunk::get 的时候. 比如在上面的例子中:

let n1 = Cell::new(1)
let n2 = Cell::new(2)
let n3 = Cell::new(3)
let t1 = Thunk::new(fn() { n1.get() + n2.get() })
let t2 = Thunk::new(fn() { t1.get() + n3.get() })
t2.get()

当用户调用 t2.get() 时, 我们在运行时会知道 t1.get() 和 n3.get() 在其中也被调用了. 因此 t1 和 n3 是 t2 的依赖, 并且我们可以构建一个这样的图:

同样的过程也会在 t1.get() 被调用时发生.

所以计划是这样的:

我们定义一个栈来记录我们当前在获得哪个 thunk 的值. 在这里使用栈的原因是, 我们事实上是在尝试记录每个 get 的调用栈.
当我们调用 get 时, 将其标记为栈顶 thunk 的依赖, 如果它是一个 thunk, 再把它压栈.
当一个 thunk 的 get 结束时, 将它出栈.

让我们看看上面那个例子在这个算法下的过程是什么样子的:

当我们调用 t2.get 时, 将 t2 压栈.
当我们在 t2.get 中调用 t1.get 时, 将 t1 记为 t2 的依赖, 并将 t1 压栈.
当我们在 t1.get 中调用 n1.get 时, 将 n1 记为 t1 的依赖
相同的过程发生在 n2 身上.
当 t1.get 结束时, 将 t1 出栈.
当我们调用 n3.get 时, 将 n3 记为 t2 的依赖.

除了这些从父依赖到子依赖的边之外, 我们最好也记录一个从子依赖到父依赖的边, 方便后面我们在这个图上反向便利.

在接下来的代码中, 我们将使用 outgoing_edges 指代从父依赖到子依赖的边, 使用 incoming_edges 指代中子依赖到父依赖的边.

如何标记过时的节点

当我们调用 Cell::set 时, 该节点本身和所有依赖它的节点都应该被标记为过时的. 这将在后面作为判断一个 thunk 是否需要重新计算的标准之一. 这基本上是一个从图的叶子节点向后遍历的过程. 我们可以用这样的伪 MoonBit 代码表示这个算法:

fn dirty(node: Node) -> Unit {
  for n in node.incoming_edges {
    n.set_dirty(true)
    dirty(node)
  }
}

如何决定一个 thunk 需要被重新计算

当我们调用 Thunk::get 时, 我们需要决定是否它需要被重新计算. 但只用我们在上一节描述的方法是不够的. 如果我们只使用是否过时这一个标准进行判断, 势必会有不需要的计算发生. 比如我们在一开始给出的例子:

n1.set(2)
n2.set(1)
inspect(t2.get(), content="6")

当我们调换 n1 和 n2 的值时, n1, n2, t1 和 t2 都应该被标记为过时, 但当我们调用 t2.get 时, 其实没有必要重新计算 t2, 因为 t1 的值并没有改变.

这提醒我们除了过时之外, 我们还要考虑依赖的值是否和它上一次的值一样. 如果一个节点既是过时的, 并且它的依赖中存在一个值和上一次不同, 那么它应该被重新计算.

我们可以用下面的伪 MoonBit 代码描述这个算法:

fn propagate(self: Node) -> Unit {
  // 当一个节点过时了, 它可能需要被重新计算
  if self.is_dirty() {
    // 重新计算之后, 它将不在是过时的
    self.set_dirty(false)
    for dependency in self.outgoing_edges() {
      // 递归地重新计算每个依赖
      dependency.propagate()
      // 如果一个依赖的值改变了, 这个节点需要被重新计算
      if dependency.is_changed() {
        // 移除所有的 outgoing_edges, 它们将在被计算时重新构建
        self.outgoing_edges().clear()
        self.evaluate()
        return
      }
    }
  }
}

实现

基于上面描述的代码, 实现是比较直观的.

首先, 我们先定义 Cell:

struct Cell[A] {
  mut Bool
is_dirty : Bool
Bool
  mut A
value : type parameter A
A
  mut Bool
is_changed : Bool
Bool
  Array[&Node]
incoming_edges : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
}

由于 Cell 只会是依赖图中的叶子节点, 所以它没有 outgoing_edges. 这里出现的特征 Node 是用来抽象依赖图中的节点的.

接着, 我们定义 Thunk:

struct Thunk[A] {
  mut Bool
is_dirty : Bool
Bool
  mut A?
value : type parameter A
A?
  mut Bool
is_changed : Bool
Bool
  () -> A
thunk : () -> type parameter A
A
  Array[&Node]
incoming_edges : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
  Array[&Node]
outgoing_edges : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
}

Thunk 的值是可选的, 因为它只有在我们第一次调用 Thunk::get 之后才会存在.

我们可以很简单地给这两个类型实现 new:

fn[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::fn[A : Eq] Cell::new(value : A) -> Cell[A]
new(A
value : type parameter A
A) -> struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A] {
  struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::{
    Bool
is_changed: false,
    A
value,
    Array[&Node]
incoming_edges: [],
    Bool
is_dirty: false,
  }
}

fn[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::fn[A : Eq] Thunk::new(thunk : () -> A) -> Thunk[A]
new(() -> A
thunk : () -> type parameter A
A) -> struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[type parameter A
A] {
  struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::{
    A?
value: A?
None,
    Bool
is_changed: false,
    () -> A
thunk,
    Array[&Node]
incoming_edges: [],
    Array[&Node]
outgoing_edges: [],
    Bool
is_dirty: false,
  }
}

Thunk 和 Cell 是依赖图的两种节点, 我们可以使用一个特征 Node 来抽象它们:

trait trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node {
  (Self) -> Bool
is_dirty(type parameter Self
Self) -> Bool
Bool
  (Self, Bool) -> Unit
set_dirty(type parameter Self
Self, Bool
Bool) -> Unit
Unit
  (Self) -> Array[&Node]
incoming_edges(type parameter Self
Self) -> type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
  (Self) -> Array[&Node]
outgoing_edges(type parameter Self
Self) -> type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node]
  (Self) -> Bool
is_changed(type parameter Self
Self) -> Bool
Bool
  (Self) -> Unit
evaluate(type parameter Self
Self) -> Unit
Unit
}

为两个类型实现这个特征:

impl[A] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A] with fn[A] Node::incoming_edges(self : Cell[A]) -> Array[&Node]
incoming_edges(Cell[A]
self) {
  Cell[A]
self.Array[&Node]
incoming_edges
}

impl[A] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A] with fn[A] Node::outgoing_edges(_self : Cell[A]) -> Array[&Node]
outgoing_edges(Cell[A]
_self) {
  []
}

impl[A] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A] with fn[A] Node::is_dirty(self : Cell[A]) -> Bool
is_dirty(Cell[A]
self) {
  Cell[A]
self.Bool
is_dirty
}

impl[A] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A] with fn[A] Node::set_dirty(self : Cell[A], new_dirty : Bool) -> Unit
set_dirty(Cell[A]
self, Bool
new_dirty) {
  Cell[A]
self.Bool
is_dirty = Bool
new_dirty
}

impl[A] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A] with fn[A] Node::is_changed(self : Cell[A]) -> Bool
is_changed(Cell[A]
self) {
  Cell[A]
self.Bool
is_changed
}

impl[A] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A] with fn[A] Node::evaluate(_self : Cell[A]) -> Unit
evaluate(Cell[A]
_self) {
  ()
}

impl[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[type parameter A
A] with fn[A : Eq] Node::is_changed(self : Thunk[A]) -> Bool
is_changed(Thunk[A]
self) {
  Thunk[A]
self.Bool
is_changed
}

impl[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[type parameter A
A] with fn[A : Eq] Node::outgoing_edges(self : Thunk[A]) -> Array[&Node]
outgoing_edges(Thunk[A]
self) {
  Thunk[A]
self.Array[&Node]
outgoing_edges
}

impl[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[type parameter A
A] with fn[A : Eq] Node::incoming_edges(self : Thunk[A]) -> Array[&Node]
incoming_edges(Thunk[A]
self) {
  Thunk[A]
self.Array[&Node]
incoming_edges
}

impl[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[type parameter A
A] with fn[A : Eq] Node::is_dirty(self : Thunk[A]) -> Bool
is_dirty(Thunk[A]
self) {
  Thunk[A]
self.Bool
is_dirty
}

impl[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[type parameter A
A] with fn[A : Eq] Node::set_dirty(self : Thunk[A], new_dirty : Bool) -> Unit
set_dirty(Thunk[A]
self, Bool
new_dirty) {
  Thunk[A]
self.Bool
is_dirty = Bool
new_dirty
}

impl[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node for struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[type parameter A
A] with fn[A : Eq] Node::evaluate(self : Thunk[A]) -> Unit
evaluate(Thunk[A]
self) {
  let node_stack : Array[&Node]
node_stack.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(Thunk[A]
self)
  let A
value = (Thunk[A]
self.() -> A
thunk)()
  Thunk[A]
self.Bool
is_changed = match Thunk[A]
self.A?
value {
    A?
None => true
    (A) -> A?
Some(A
v) => A
v fn[T : Eq] @moonbitlang/core/builtin.op_notequal(x : T, y : T) -> Bool
!= A
value
  }
  Thunk[A]
self.A?
value = (A) -> A?
Some(A
value)
  let node_stack : Array[&Node]
node_stack.fn[T] Array::unsafe_pop(self : Array[T]) -> T
Removes and returns the last element from the array.
Parameters:

array : The array from which to remove and return the last element.
Returns the last element of the array before removal.
Example:
let arr = [1, 2, 3]
inspect(arr.unsafe_pop(), content="3")
inspect(arr, content="[1, 2]")
unsafe_pop() |> fn[T] ignore(t : T) -> Unit
Evaluates an expression and discards its result. This is useful when you want
to execute an expression for its side effects but don't care about its return
value, or when you want to explicitly indicate that a value is intentionally
unused.
Parameters:

value : The value to be ignored. Can be of any type.
Example:
let x = 42
ignore(x) // Explicitly ignore the value
let mut sum = 0
ignore([1, 2, 3].iter().each(x => sum = sum + x)) // Ignore the Unit return value of each()
ignore
}

这里唯一复杂的实现是 Thunk 的 evaluate. 这里我们需要先把这个 thunk 推到栈顶用于后面的依赖记录. node_stack 的定义如下:

let Array[&Node]
node_stack : type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[&trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node] = []

然后做真正的计算, 并且把计算得到的值和上一个值做比较以更新 self.is_changed. is_changed 会在后面帮助我们判断是否需要重新计算一个 thunk.

dirty 和 propagate 的实现几乎和上面的伪代码相同:

fn trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
&Node::fn Node::dirty(self : &Node) -> Unit
dirty(&Node
self : &trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node) -> Unit
Unit {
  for &Node
dependent in &Node
self.fn Node::incoming_edges(&Node) -> Array[&Node]
incoming_edges() {
    if fn not(x : Bool) -> Bool
Performs logical negation on a boolean value.
Parameters:

value : The boolean value to negate.
Returns the logical NOT of the input value: true if the input is false,
and false if the input is true.
Example:
inspect(not(true), content="false")
inspect(not(false), content="true")
not(&Node
dependent.fn Node::is_dirty(&Node) -> Bool
is_dirty()) {
      &Node
dependent.fn Node::set_dirty(&Node, Bool) -> Unit
set_dirty(true)
      &Node
dependent.fn Node::dirty(self : &Node) -> Unit
dirty()
    }
  }
}

fn trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
&Node::fn Node::propagate(self : &Node) -> Unit
propagate(&Node
self : &trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
Node) -> Unit
Unit {
  if &Node
self.fn Node::is_dirty(&Node) -> Bool
is_dirty() {
    &Node
self.fn Node::set_dirty(&Node, Bool) -> Unit
set_dirty(false)
    for &Node
dependency in &Node
self.fn Node::outgoing_edges(&Node) -> Array[&Node]
outgoing_edges() {
      &Node
dependency.fn Node::propagate(self : &Node) -> Unit
propagate()
      if &Node
dependency.fn Node::is_changed(&Node) -> Bool
is_changed() {
        &Node
self.fn Node::outgoing_edges(&Node) -> Array[&Node]
outgoing_edges().fn[T] Array::clear(self : Array[T]) -> Unit
Clears the array, removing all values.
This method has no effect on the allocated capacity of the array, only setting the length to 0.
Example
  let v = [3, 4, 5]
  v.clear()
  assert_eq(v.length(), 0)
clear()
        &Node
self.fn Node::evaluate(&Node) -> Unit
evaluate()
        return
      }
    }
  }
}

有了这些函数的帮助, 最主要的三个 API: Cell::get, Cell::set 和 Thunk::get 实现起来就比较简单了.

为了得到一个 cell 的值, 我们直接返回结构体的 value 字段即可. 但在此之前, 如果它是在一个 Thunk::get 中被调用的, 我们要先把他记录为依赖.

fn[A] struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::fn[A] Cell::get(self : Cell[A]) -> A
get(Cell[A]
self : struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A]) -> type parameter A
A {
  if let node_stack : Array[&Node]
node_stack.fn[A] Array::last(self : Array[A]) -> A?
Returns the last element of the array, or None if the array is empty.
Parameters:

array : The array to get the last element from.
Returns an optional value containing the last element of the array. The
result is None if the array is empty, or Some(x) where x is the last
element of the array.
Example:
let arr = [1, 2, 3]
inspect(arr.last(), content="Some(3)")
let empty : Array[Int] = []
inspect(empty.last(), content="None")
last() is (&Node) -> &Node?
Some(&Node
target) {
    &Node
target.fn Node::outgoing_edges(&Node) -> Array[&Node]
outgoing_edges().fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(Cell[A]
self)
    Cell[A]
self.Array[&Node]
incoming_edges.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(&Node
target)
  }
  Cell[A]
self.A
value
}

当我们更改一个 cell 的值时, 我们需要先确保 is_changed 和 dirty 这两个状态被正确地更新了, 再将它的每一个父依赖标记为过时.

fn[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell::fn[A : Eq] Cell::set(self : Cell[A], new_value : A) -> Unit
set(Cell[A]
self : struct Cell[A] {
  mut is_dirty: Bool
  mut value: A
  mut is_changed: Bool
  incoming_edges: Array[&Node]
}
Cell[type parameter A
A], A
new_value : type parameter A
A) -> Unit
Unit {
  if Cell[A]
self.A
value fn[T : Eq] @moonbitlang/core/builtin.op_notequal(x : T, y : T) -> Bool
!= A
new_value {
    Cell[A]
self.Bool
is_changed = true
    Cell[A]
self.A
value = A
new_value
    Cell[A]
self.fn[A] Node::set_dirty(self : Cell[A], new_dirty : Bool) -> Unit
set_dirty(true)
    trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
&Node::fn Node::dirty(self : &Node) -> Unit
dirty(Cell[A]
self)
  }
}

和 Cell::get 类似, 在实现 Thunk::get 时我们需要先将 self 记录为依赖. 之后我们模式匹配 self.value, 如果它是 None, 这意味着这是第一次用户尝试计算这个 thunk 地值, 我们可以简单地直接计算它; 如果它是 Some, 我们需要使用 propagate 来确保我们只重新计算那些需要的 thunk.

fn[A : trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq] struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk::fn[A : Eq] Thunk::get(self : Thunk[A]) -> A
get(Thunk[A]
self : struct Thunk[A] {
  mut is_dirty: Bool
  mut value: A?
  mut is_changed: Bool
  thunk: () -> A
  incoming_edges: Array[&Node]
  outgoing_edges: Array[&Node]
}
Thunk[type parameter A
A]) -> type parameter A
A {
  if let node_stack : Array[&Node]
node_stack.fn[A] Array::last(self : Array[A]) -> A?
Returns the last element of the array, or None if the array is empty.
Parameters:

array : The array to get the last element from.
Returns an optional value containing the last element of the array. The
result is None if the array is empty, or Some(x) where x is the last
element of the array.
Example:
let arr = [1, 2, 3]
inspect(arr.last(), content="Some(3)")
let empty : Array[Int] = []
inspect(empty.last(), content="None")
last() is (&Node) -> &Node?
Some(&Node
target) {
    &Node
target.fn Node::outgoing_edges(&Node) -> Array[&Node]
outgoing_edges().fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(Thunk[A]
self)
    Thunk[A]
self.Array[&Node]
incoming_edges.fn[T] Array::push(self : Array[T], value : T) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(&Node
target)
  }
  match Thunk[A]
self.A?
value {
    A?
None => Thunk[A]
self.fn[A : Eq] Node::evaluate(self : Thunk[A]) -> Unit
evaluate()
    (A) -> A?
Some(_) => trait Node {
  is_dirty(Self) -> Bool
  set_dirty(Self, Bool) -> Unit
  incoming_edges(Self) -> Array[&Node]
  outgoing_edges(Self) -> Array[&Node]
  is_changed(Self) -> Bool
  evaluate(Self) -> Unit
}
&Node::fn Node::propagate(self : &Node) -> Unit
propagate(Thunk[A]
self)
  }
  Thunk[A]
self.A?
value.fn[X] Option::unwrap(self : X?) -> X
Extract the value in Some.
If the value is None, it throws a panic.
unwrap()
}

参考

Adapton: Composable, demand-driven incremental computation, PLDI 2014 adapton 的原论文
illusory0x0/adapton.mbt adapton 库的 MoonBit 实现

MoonBit与Python集成指南

2025年8月19日 · 阅读需 13 分钟

引言

Python，以其简洁的语法和庞大的生态系统，已成为当今最受欢迎的编程语言之一。然而，围绕其性能瓶颈和动态类型系统在大型项目中的维护性问题的讨论也从未停止。为了解决这些挑战，开发者社区探索了多种优化路径。

MoonBit 官方推出的 python.mbt 工具为此提供了一个新的视角。它允许开发者在 MoonBit 环境中直接调用 Python 代码。这种结合旨在融合 MoonBit 的静态类型安全、高性能潜力与 Python 成熟的生态系统。通过 python.mbt，开发者可以在享受 Python 丰富库函数的同时，利用 MoonBit 的静态分析能力、现代化的构建与测试工具，为构建大规模、高性能的系统级软件提供可能。

本文旨在深入探讨 python.mbt 的工作原理，并提供一份实践指南。本文将解答一些常见问题，例如：python.mbt 如何工作？它是否会因为增加了一个中间层而比原生 Python 更慢？相较于 C++ 的 pybind11 或 Rust 的 PyO3 等现有工具，python.mbt 的优势何在？要回答这些问题，我们首先需要理解 Python 解释器的基本工作流程。

Python 解释器的工作原理

Python 解释器执行代码主要经历三个阶段：

解析阶段 (Parsing) ：此阶段包含词法分析和语法分析。解释器将人类可读的 Python 源代码分解成一个个标记（Token），然后根据语法规则将这些标记组织成一个树形结构，即抽象语法树（AST）。

例如，对于以下 Python 代码：

def add(x, y):
  return x + y

a = add(1, 2)
print(a)

我们可以使用 Python 的 ast 模块来查看其生成的 AST 结构：

Module(
    body=[
        FunctionDef(
            name='add',
            args=arguments(
                args=[
                    arg(arg='x'),
                    arg(arg='y')]),
            body=[
                Return(
                    value=BinOp(
                        left=Name(id='x', ctx=Load()),
                        op=Add(),
                        right=Name(id='y', ctx=Load())))]),
        Assign(
            targets=[
                Name(id='a', ctx=Store())],
            value=Call(
                func=Name(id='add', ctx=Load()),
                args=[
                    Constant(value=1),
                    Constant(value=2)])),
        Expr(
            value=Call(
                func=Name(id='print', ctx=Load()),
                args=[
                    Name(id='a', ctx=Load())]))])

编译阶段 (Compilation) ：接下来，Python 解释器会将 AST 编译成更低级、更线性的中间表示，即字节码（Bytecode）。这是一种平台无关的指令集，专为 Python 虚拟机（PVM）设计。

利用 Python 的 dis 模块，我们可以查看上述代码对应的字节码：

  2           LOAD_CONST               0 (<code object add>)
              MAKE_FUNCTION
              STORE_NAME               0 (add)

  5           LOAD_NAME                0 (add)
              PUSH_NULL
              LOAD_CONST               1 (1)
              LOAD_CONST               2 (2)
              CALL                     2
              STORE_NAME               1 (a)

  6           LOAD_NAME                2 (print)
              PUSH_NULL
              LOAD_NAME                1 (a)
              CALL                     1
              POP_TOP
              RETURN_CONST             3 (None)

执行阶段 (Execution) ：最后，Python 虚拟机（PVM）会逐条执行字节码指令。每条指令都对应 CPython 解释器底层的一个 C 函数调用。例如，LOAD_NAME 会查找变量，BINARY_OP 会执行二元运算。正是这个逐条解释执行的过程，构成了 Python 性能开销的主要来源。一次简单的 1 + 2 运算，背后需要经历整个解析、编译和虚拟机执行的复杂流程。

了解这个流程，有助于我们理解 Python 性能优化的基本思路，以及 python.mbt 的设计哲学。

优化 Python 性能的路径

目前，提升 Python 程序性能主要有两种主流方法：

即时编译（JIT） 。像 PyPy 这样的项目，通过分析正在运行的程序，将频繁执行的"热点"字节码编译成高度优化的本地机器码，从而绕过 PVM 的解释执行，大幅提升计算密集型任务的速度。然而，JIT 并非万能药，它无法解决 Python 动态类型语言的固有问题，例如在大型项目中难以进行有效的静态分析，这给软件维护带来了挑战。
原生扩展。开发者可以使用 C++（借助 pybind11）或 Rust（借助 PyO3）等语言直接调用Python功能，或者用这些语言来编写性能关键模块，然后从 Python 中调用。这种方法可以获得接近原生的性能，但它要求开发者同时精通 Python 和一门复杂的系统级语言，学习曲线陡峭，对大多数 Python 程序员来说门槛较高。

python.mbt 也是一种原生扩展。但相比较于C++和Rust等语言，它试图在性能、易用性和工程化能力之间找到一个新的平衡点，更强调在MoonBit语言中直接使用Python功能。

高性能核心：MoonBit 是一门静态类型的编译型语言，其代码可以被高效地编译成原生机器码。开发者可以将计算密集型逻辑用 MoonBit 实现，从根本上获得高性能。
无缝的 Python 调用：python.mbt 直接与 CPython 的 C-API 交互，调用 Python 模块和函数。这意味着调用开销被最小化，绕过了 Python 的解析和编译阶段，直达虚拟机执行层。
更平缓的学习曲线：相较于 C++ 和 Rust，MoonBit 的语法设计更加现代化和简洁，并拥有完善的函数式编程支持、文档系统、单元测试和静态分析工具，对习惯于 Python 的开发者更加友好。
改善的工程化与 AI 协作：MoonBit 的强类型系统和清晰的接口定义，使得代码意图更加明确，更易于被静态分析工具和 AI 辅助编程工具理解。这有助于在大型项目中维护代码质量，并提升与 AI 协作编码的效率和准确性。

在 MoonBit 中使用已封装的 Python 库

为了方便开发者使用，MoonBit 官方会在构建系统和IDE成熟后对主流 Python 库进行封装。封装完成后，用户可以像导入普通 MoonBit 包一样，在项目中使用这些 Python 库。下面以 matplotlib 绘图库为例。

首先，在你的项目根目录的 moon.pkg.json 或终端中添加 matplotlib 依赖：

moon update
moon add Kaida-Amethyst/matplotlib

然后，在要使用该库的子包的 moon.pkg.json 中声明导入。这里，我们遵循 Python 的惯例，为其设置一个别名 plt：

{
  "import": [
    {
      "path": "Kaida-Amethyst/matplotlib",
      "alias": "plt"
    }
  ]
}

完成配置后，便可以在 MoonBit 代码中调用 matplotlib 进行绘图：

let (Double) -> Double
sin : (Double
Double) -> Double
Double = fn @moonbitlang/core/math.sin(x : Double) -> Double
Calculates the sine of a number in radians. Handles special cases and edge
conditions according to IEEE 754 standards.
Parameters:

x : The angle in radians for which to calculate the sine.
Returns the sine of the angle x.
Example:
inspect(@math.sin(0.0), content="0")
inspect(@math.sin(1.570796326794897), content="1") // pi / 2
inspect(@math.sin(2.0), content="0.9092974268256817")
inspect(@math.sin(-5.0), content="0.9589242746631385")
inspect(@math.sin(31415926535897.9323846), content="0.0012091232715481885")
inspect(@math.sin(@double.not_a_number), content="NaN")
inspect(@math.sin(@double.infinity), content="NaN")
inspect(@math.sin(@double.neg_infinity), content="NaN")
@math.sin

fn main {
  let Array[Double]
x = type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array::fn[T] Array::makei(length : Int, value : (Int) -> T raise?) -> Array[T] raise?
Creates a new array of the specified length, where each element is
initialized using an index-based initialization function.
Parameters:

length : The length of the new array. If length is less than or equal
to 0, returns an empty array.
initializer : A function that takes an index (starting from 0) and
returns a value of type T. This function is called for each index to
initialize the corresponding element.
Returns a new array of type Array[T] with the specified length, where each
element is initialized using the provided function.
Example:
let arr = Array::makei(3, i => i * 2)
inspect(arr, content="[0, 2, 4]")
makei(100, fn(Int
i) { Int
i.fn Int::to_double(self : Int) -> Double
Converts a 32-bit integer to a double-precision floating-point number. The
conversion preserves the exact value since all integers in the range of Int
can be represented exactly as Double values.
Parameters:

self : The 32-bit integer to be converted.
Returns a double-precision floating-point number that represents the same
numerical value as the input integer.
Example:
let n = 42
inspect(n.to_double(), content="42")
let neg = -42
inspect(neg.to_double(), content="-42")
to_double() fn Mul::mul(self : Double, other : Double) -> Double
Multiplies two double-precision floating-point numbers. This is the
implementation of the * operator for Double type.
Parameters:

self : The first double-precision floating-point operand.
other : The second double-precision floating-point operand.
Returns a new double-precision floating-point number representing the product
of the two operands. Special cases follow IEEE 754 standard:

If either operand is NaN, returns NaN
If one operand is infinity and the other is zero, returns NaN
If one operand is infinity and the other is a non-zero finite number,
returns infinity with the appropriate sign
If both operands are infinity, returns infinity with the appropriate sign
Example:
inspect(2.5 * 2.0, content="5")
inspect(-2.0 * 3.0, content="-6")
let nan = 0.0 / 0.0 // NaN
inspect(nan * 1.0, content="NaN")
* 0.1 })
  let Array[Double]
y = Array[Double]
x.fn[T, U] Array::map(self : Array[T], f : (T) -> U raise?) -> Array[U] raise?
Maps a function over the elements of the array.
Example
  let v = [3, 4, 5]
  let v2 = v.map((x) => {x + 1})
  assert_eq(v2, [4, 5, 6])
map(let sin : (Double) -> Double
sin)

  // 为保证类型安全，封装后的 subplots 接口总是返回一个固定类型的元组。
  // 这避免了 Python 中根据参数返回不同类型对象的动态行为。
  let (_, Unit
axes) = (Int, Int) -> (Unit, Unit)
plt::(Int, Int) -> (Unit, Unit)
subplots(1, 1)

  // 使用 .. 级联调用语法
  Unit
axes[0(Int) -> Unit
][0]
  ..(Array[Double], Array[Double], Unit, Unit, Int) -> Unit
plot(Array[Double]
x, Array[Double]
y, Unit
color = Unit
Green, Unit
linestyle = Unit
Dashed, Int
linewidth = 2)
  ..(String) -> Unit
set_title("Sine of x")
  ..(String) -> Unit
set_xlabel("x")
  ..(String) -> Unit
set_ylabel("sin(x)")

  () -> Unit
@plt.show()
}

目前，在 macOS 和 Linux 环境下，MoonBit 的构建系统可以自动处理依赖。在 Windows 上，用户可能需要手动安装 C 编译器并配置 Python 环境。未来的 MoonBit IDE 将致力于简化这一过程。

在 MoonBit 中使用未封装的 Python 模块

Python 生态浩如烟海，即使现在有了AI技术，完全依赖官方封装也并不现实。幸运的是，我们可以利用 python.mbt 的核心功能直接与任何 Python 模块交互。下面，我们以 Python 标准库中，一个简单的的 time 模块为例，演示这一过程。

引入 python.mbt

首先，确保你的 MoonBit 工具链是最新版本，然后添加 python.mbt 依赖：

moon update
moon add Kaida-Amethyst/python

接着，在你的包的 moon.pkg.json 中导入它：

{
  "import": ["Kaida-Amethyst/python"]
}

python.mbt 会自动处理 Python 解释器的初始化（Py_Initialize）和关闭，开发者无需手动管理。

导入 Python 模块

使用 @python.pyimport 函数来导入模块。为了避免重复导入造成的性能损耗，建议使用闭包技巧来缓存导入的模块对象：

// 定义一个结构体来持有 Python 模块对象，增强类型安全
pub struct TimeModule {
  ?
time_mod: PyModule
}

// 定义一个函数，它返回一个闭包，该闭包用于获取 TimeModule 实例
fn fn import_time_mod() -> () -> TimeModule
import_time_mod() -> () -> struct TimeModule {
  time_mod: ?
}
TimeModule {
  // 仅在首次调用时执行导入操作
  guard (String) -> Unit
@python.pyimport("time") is (?) -> Unit
Some(?
time_mod) else {
    fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("Failed to load Python module: time")
    fn[T] panic() -> T
panic("ModuleLoadError")
  }
  let TimeModule
time_mod = struct TimeModule {
  time_mod: ?
}
TimeModule::{ ?
time_mod }
  // 返回的闭包会捕获 time_mod 变量
  fn () { TimeModule
time_mod }
}

// 创建一个全局的 time_mod "getter" 函数
let () -> TimeModule
time_mod: () -> struct TimeModule {
  time_mod: ?
}
TimeModule = fn import_time_mod() -> () -> TimeModule
import_time_mod()

在后续代码中，我们应始终通过调用 time_mod() 来获取模块，而不是 import_time_mod。

MoonBit 与 Python 对象的相互转换

要调用 Python 函数，我们需要在 MoonBit 对象和 Python 对象（PyObject）之间进行转换。

整数: 使用 PyInteger::from 从 Int64 创建 PyInteger，使用 to_int64() 反向转换。

test "py_integer_conversion" {
  let Int64
n: Int64
Int64 = 42
  let &Show
py_int = (Int64) -> &Show
PyInteger::(Int64) -> &Show
from(Int64
n)
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(&Show
py_int, String
content="42")
  fn[T : Eq + Show] assert_eq(a : T, b : T, msg? : String, loc~ : SourceLoc = _) -> Unit raise
Asserts that two values are equal. If they are not equal, raises a failure
with a message containing the source location and the values being compared.
Parameters:

a : First value to compare.
b : Second value to compare.
loc : Source location information to include in failure messages. This is
usually automatically provided by the compiler.
Throws a Failure error if the values are not equal, with a message showing
the location of the failing assertion and the actual values that were
compared.
Example:
assert_eq(1, 1)
assert_eq("hello", "hello")
assert_eq(&Show
py_int.() -> Int64
to_int64(), 42L)
}

浮点数: 使用 PyFloat::from 和 to_double。

test "py_float_conversion" {
  let Double
n: Double
Double = 3.5
  let &Show
py_float = (Double) -> &Show
PyFloat::(Double) -> &Show
from(Double
n)
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(&Show
py_float, String
content="3.5")
  fn[T : Eq + Show] assert_eq(a : T, b : T, msg? : String, loc~ : SourceLoc = _) -> Unit raise
Asserts that two values are equal. If they are not equal, raises a failure
with a message containing the source location and the values being compared.
Parameters:

a : First value to compare.
b : Second value to compare.
loc : Source location information to include in failure messages. This is
usually automatically provided by the compiler.
Throws a Failure error if the values are not equal, with a message showing
the location of the failing assertion and the actual values that were
compared.
Example:
assert_eq(1, 1)
assert_eq("hello", "hello")
assert_eq(&Show
py_float.() -> Double
to_double(), 3.5)
}

字符串: 使用 PyString::from 和 to_string。

test "py_string_conversion" {
  let &Show
py_str = (String) -> &Show
PyString::(String) -> &Show
from("hello")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(&Show
py_str, String
content="'hello'")
  fn[T : Eq + Show] assert_eq(a : T, b : T, msg? : String, loc~ : SourceLoc = _) -> Unit raise
Asserts that two values are equal. If they are not equal, raises a failure
with a message containing the source location and the values being compared.
Parameters:

a : First value to compare.
b : Second value to compare.
loc : Source location information to include in failure messages. This is
usually automatically provided by the compiler.
Throws a Failure error if the values are not equal, with a message showing
the location of the failing assertion and the actual values that were
compared.
Example:
assert_eq(1, 1)
assert_eq("hello", "hello")
assert_eq(&Show
py_str.fn Show::to_string(&Show) -> String
to_string(), "hello")
}

列表 (List) : 你可以创建一个空 PyList 然后 append 元素，或者直接从一个 Array[&IsPyObject] 创建。

test "py_list_from_array" {
  let Unit
one = (Int) -> Unit
PyInteger::(Int) -> Unit
from(1)
  let Unit
two = (Double) -> Unit
PyFloat::(Double) -> Unit
from(2.0)
  let Unit
three = (String) -> Unit
PyString::(String) -> Unit
from("three")
  let Array[Unit]
arrArray[Unit]
: type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
ArrayArray[Unit]
[&IsPyObject] = [Unit
one, Unit
two, Unit
three]

  let &Show
list = (Array[Unit]) -> &Show
PyList::(Array[Unit]) -> &Show
from(Array[Unit]
arr)
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(&Show
list, String
content="[1, 2.0, 'three']")
}

元组 (Tuple) : PyTuple 需要先指定大小，然后通过 set 方法逐一填充元素。

test "py_tuple_creation" {
  let &Show
tuple = (Int) -> &Show
PyTuple::(Int) -> &Show
new(3)
  &Show
tuple
  ..(Int, Unit) -> Unit
set(0, (Int) -> Unit
PyInteger::(Int) -> Unit
from(1))
  ..(Int, Unit) -> Unit
set(1, (Double) -> Unit
PyFloat::(Double) -> Unit
from(2.0))
  ..(Int, Unit) -> Unit
set(2, (String) -> Unit
PyString::(String) -> Unit
from("three"))

  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(&Show
tuple, String
content="(1, 2.0, 'three')")
}

字典 (Dict) : PyDict 主要支持字符串作为键。使用 new 创建字典，set 添加键值对。对于非字符串键，需要使用 set_by_obj。

test "py_dict_creation" {
  let &Show
dict = () -> &Show
PyDict::() -> &Show
new()
  &Show
dict
  ..(String, Unit) -> Unit
set("one", (Int) -> Unit
PyInteger::(Int) -> Unit
from(1))
  ..(String, Unit) -> Unit
set("two", (Double) -> Unit
PyFloat::(Double) -> Unit
from(2.0))

  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(&Show
dict, String
content="{'one': 1, 'two': 2.0}")
}

从 Python 复合类型中获取元素时，python.mbt 会进行运行时类型检查，并返回一个 Optional[PyObjectEnum]，以确保类型安全。

test "py_list_get" {
  let Unit
list = () -> Unit
PyList::() -> Unit
new()
  Unit
list.(Unit) -> Unit
append((Int) -> Unit
PyInteger::(Int) -> Unit
from(1))
  Unit
list.(Unit) -> Unit
append((String) -> Unit
PyString::(String) -> Unit
from("hello"))

  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Unit
list.(Int) -> Unit
get(0).() -> &Show
unwrap(), String
content="PyInteger(1)")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Unit
list.(Int) -> Unit
get(1).() -> &Show
unwrap(), String
content="PyString('hello')")
  fn inspect(obj : &Show, content~ : String, loc~ : SourceLoc = _, args_loc~ : ArgsLoc = _) -> Unit raise InspectError
Tests if the string representation of an object matches the expected content.
Used primarily in test cases to verify the correctness of Show
implementations and program outputs.
Parameters:

object : The object to be inspected. Must implement the Show trait.
content : The expected string representation of the object. Defaults to
an empty string.
location : Source code location information for error reporting.
Automatically provided by the compiler.
arguments_location : Location information for function arguments in
source code. Automatically provided by the compiler.
Throws an InspectError if the actual string representation of the object
does not match the expected content. The error message includes detailed
information about the mismatch, including source location and both expected
and actual values.
Example:
inspect(42, content="42")
inspect("hello", content="hello")
inspect([1, 2, 3], content="[1, 2, 3]")
inspect(Unit
list.(Int) -> &Show
get(2), String
content="None") // 索引越界返回 None
}

调用模块中的函数

调用函数分为两步：首先用 get_attr 获取函数对象，然后用 invoke 执行调用。invoke 的返回值是一个需要进行模式匹配和类型转换的 PyObject。

下面是 time.sleep 和 time.time 的 MoonBit 封装：

// 封装 time.sleep
pub fn fn sleep(seconds : Double) -> Unit
sleep(Double
seconds: Double
Double) -> Unit
Unit {
  let TimeModule
lib = let time_mod : () -> TimeModule
time_mod()
  guard TimeModule
lib.?
time_mod.(String) -> Unit
get_attr("sleep") is (_/0) -> Unit
Some((Unit) -> _/0
PyCallable(Unit
f)) else {
    fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("get function `sleep` failed!")
    fn[T] panic() -> T
panic()
  }
  let Unit
args = (Int) -> Unit
PyTuple::(Int) -> Unit
new(1)
  Unit
args.(Int, Unit) -> Unit
set(0, (Double) -> Unit
PyFloat::(Double) -> Unit
from(Double
seconds))
  match (try? Unit
f.(Unit) -> Unit
invoke(Unit
args)) {
    (Unit) -> Result[Unit, Error]
Ok(_) => Unit
Ok(())
    (Error) -> Result[Unit, Error]
Err(Error
e) => {
      fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("invoke `sleep` failed!")
      fn[T] panic() -> T
panic()
    }
  }
}

// 封装 time.time
pub fn fn time() -> Double
time() -> Double
Double {
  let TimeModule
lib = let time_mod : () -> TimeModule
time_mod()
  guard TimeModule
lib.?
time_mod.(String) -> Unit
get_attr("time") is (_/0) -> Unit
Some((Unit) -> _/0
PyCallable(Unit
f)) else {
    fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("get function `time` failed!")
    fn[T] panic() -> T
panic()
  }
  match (try? Unit
f.() -> Unit
invoke()) {
    (Unit) -> Result[Unit, Error]
Ok((_/0) -> Unit
Some((Unit) -> _/0
PyFloat(Unit
t))) => Unit
t.() -> Double
to_double()
    _ => {
      fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("invoke `time` failed!")
      fn[T] panic() -> T
panic()
    }
  }
}

完成封装后，我们就可以在 MoonBit 中以类型安全的方式使用它们了：

test "sleep" {
  let Unit
start = fn time() -> Double
time().() -> Unit
unwrap()
  fn sleep(seconds : Double) -> Unit
sleep(1)
  let Unit
end = fn time() -> Double
time().() -> Unit
unwrap()

  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("start = \{Unit
start}")
  fn[T : Show] println(input : T) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("end = \{Unit
end}")
}

实践建议

明确边界：将 python.mbt 视为连接 MoonBit 和 Python 生态的"胶水层"。将核心计算和业务逻辑保留在 MoonBit 中以利用其性能和类型系统优势，仅在必要情况下，需要调用 Python 独有库时才使用 python.mbt。
用 ADT 替代字符串魔法：许多 Python 函数接受特定的字符串作为参数来控制行为。在 MoonBit 封装中，应将这些"魔法字符串"转换为代数数据类型（ADT） ，即枚举。这利用了 MoonBit 的类型系统，将运行时的值检查提前到编译时，极大地增强了代码的健壮性。
完善的错误处理：本文中的示例为了简洁使用了 panic 或返回简单字符串。在生产代码中，应定义专门的错误类型，并通过 Result 类型进行传递和处理，提供清晰的错误上下文。

映射关键字参数：Python 函数广泛使用关键字参数（kwargs），如 plot(color='blue', linewidth=2)。这可以优雅地映射到 MoonBit 的标签参数（Labeled Arguments） 。在封装时，应优先使用标签参数以提供相似的开发体验。

例如，一个接受 kwargs 的 Python 函数：

# graphics.py
def draw_line(points, color="black", width=1):
    # ... drawing logic ...
    print(f"Drawing line with color {color} and width {width}")

其 MoonBit 封装可以设计成：

fn draw_line(points: Array[Point], color~: Color = Black, width: Int = 1) -> Unit {
  let points : PyList = ... // convert Array[Point] to PyList

  // 构造args
  let args = PyTuple::new(1)
  args .. set(0, points)

  // 构造kwargs
  let kwargs = PyDict::new()
  kwargs
  ..set("color", PyString::from(color))
  ...set("width", PyInteger::from(width))
  match (try? f.invoke(args~, kwargs~)) {
    Ok(_) => ()
    _ => {
      // 进行错误处理
    }
  }
}

警惕动态性：始终牢记 Python 是动态类型的。从 Python 获取的任何数据都应被视为"不可信"的，必须进行严格的类型检查和校验，尽量避免使用 unwrap，而是通过模式匹配来安全地处理所有可能的情况。

结语

本文梳理了 python.mbt 的工作原理，并展示了如何利用它在 MoonBit 中调用 Python 代码，无论是通过预封装的库还是直接与 Python 模块交互。python.mbt 不仅仅是一个工具，它代表了一种融合思想：将 MoonBit 的静态分析、高性能和工程化优势与 Python 庞大而成熟的生态系统相结合。我们希望这篇文章能为 MoonBit 和 Python 社区的开发者们在构建未来软件时，提供一个新的、更强大的选择。

二叉字典树​

Patricia Tree​

插入与合并​

Big-endian Patricia Tree​

原实现中的一处错误​

什么是 Shunting Yard 算法？​

Shunting Yard 算法的基本流程​

演算示例​

在 MoonBit 中实现 Shunting Yard 算法​

Example

Example

Example

Example

Example

Example

Example

Example

Example

Example

Example

小结​

wassette 和 MCP 简介​

总体流程​

第1步：安装必要工具​

第2步：定义接口​

创建 wit/deps.toml​

创建 wit/world.wit​

第3步：生成代码​

第4步：修改生成的代码​

Example

第5步：构建项目​

第6步（可选）：配置安全策略​

第7步：与 AI 交互​

总结​

哈希表的内部构造​

哈希冲突​

Example

制造一场冲突​

Example

哈希洪泛攻击​

缓解哈希洪泛攻击​

带"种子"的哈希函数​

其他选择​

这为什么对我们很重要？​

总结​

Footnotes​

异步编程简史​

MoonBit 中的异步编程​

HTTP 服务器的骨架​

处理用户来自用户的请求​

Examples

Examples

实现将文件夹打包成 zip 的功能​

让服务器跑起来​

引言​

预先准备​

编译项目​

第一个 JavaScript API 调用​

JavaScript 类型的对接​

无需转换的 JavaScript 类型​

外部 JavaScript 类型​

处理 JavaScript 错误​

对接外部 JavaScript API​

结语​

约定与定义​

Brzozowski 导数方法​

Example

虚拟机方法​

指令集与程序表示​

Example

AST 到字节码的编译​

虚拟机执行循环​

Example

Example

Example

Example

Parameters

Panics

Example

基准测试与性能分析​

二叉字典树

Patricia Tree

插入与合并

Big-endian Patricia Tree

原实现中的一处错误

什么是 Shunting Yard 算法？

Shunting Yard 算法的基本流程

演算示例

在 MoonBit 中实现 Shunting Yard 算法

小结

wassette 和 MCP 简介

总体流程

第1步：安装必要工具

第2步：定义接口

创建 wit/deps.toml

创建 wit/world.wit

第3步：生成代码

第4步：修改生成的代码

第5步：构建项目

第6步（可选）：配置安全策略

第7步：与 AI 交互

总结

哈希表的内部构造

哈希冲突

制造一场冲突

哈希洪泛攻击

缓解哈希洪泛攻击

带"种子"的哈希函数

其他选择

这为什么对我们很重要？

总结

Footnotes

异步编程简史

MoonBit 中的异步编程

HTTP 服务器的骨架

处理用户来自用户的请求

实现将文件夹打包成 zip 的功能

让服务器跑起来

引言

预先准备

编译项目

第一个 JavaScript API 调用

JavaScript 类型的对接

无需转换的 JavaScript 类型

外部 JavaScript 类型

处理 JavaScript 错误

对接外部 JavaScript API

结语

约定与定义

Brzozowski 导数方法

虚拟机方法

指令集与程序表示

AST 到字节码的编译

虚拟机执行循环

基准测试与性能分析

计算所需空间

实现 ExtendDoc::render

softline & softbreak

autoline & autobreak

sepby

surround

介绍

问题分析和解法

如何在运行时构建依赖图

如何标记过时的节点

如何决定一个 thunk 需要被重新计算

实现

参考

引言

Python 解释器的工作原理

优化 Python 性能的路径

在 MoonBit 中使用已封装的 Python 库

在 MoonBit 中使用未封装的 Python 模块

引入 python.mbt

导入 Python 模块

MoonBit 与 Python 对象的相互转换

调用模块中的函数

实践建议

结语